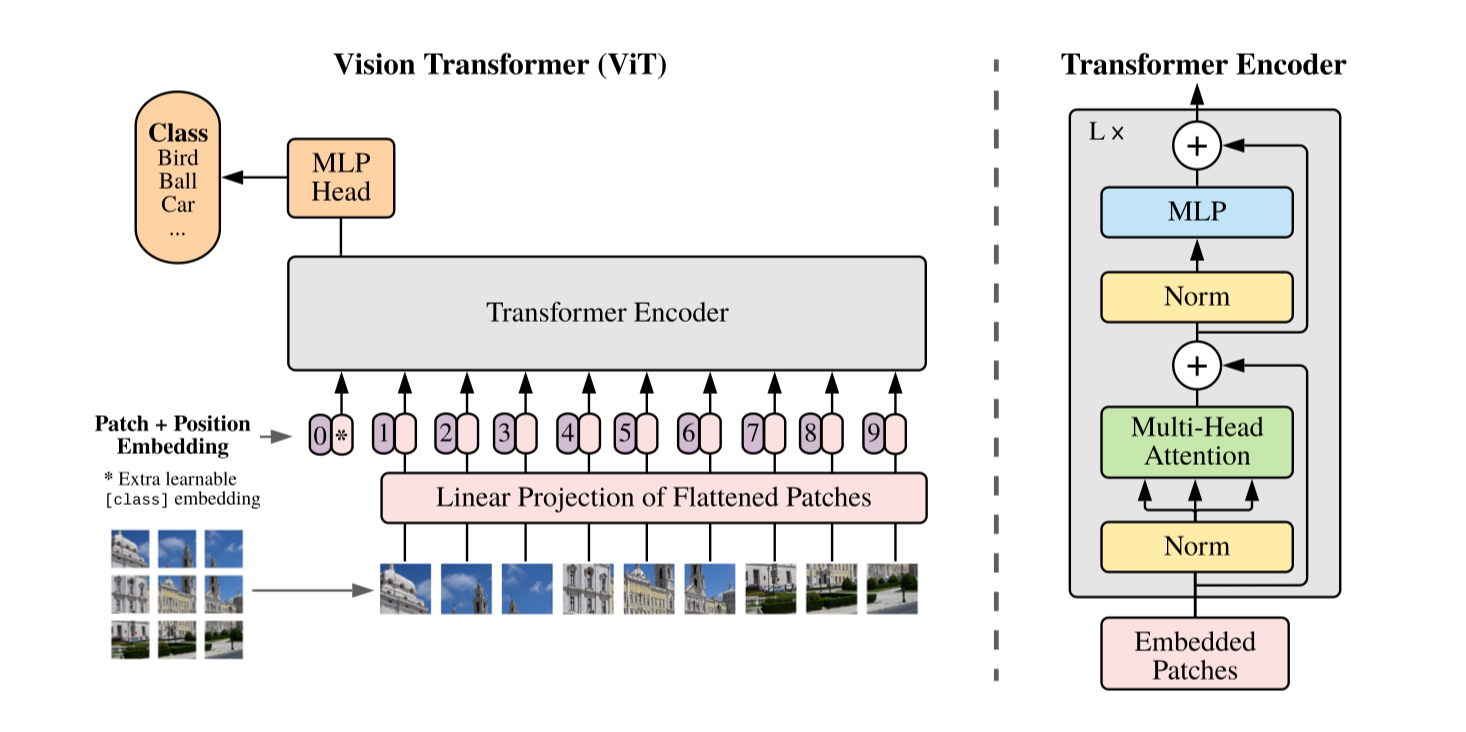
Deep Learning for Robot Perception and Cognition笔记(chapter 9)
9 Progressive and compressive learning
9.1 Introduction
提出深度神经网络的发展和困难(耗费大量时间在人工设计网络架构)。再提出NAS(Progressive neural network learning)及其优点。
随后提出深度神经网络在实际部署中存在的困难(复杂度高,性能不够),因此需要降低复杂度的方法,于是提出了model compressive 和 一些将硬件感知的运行复杂度作为最小化目标的NAS算法可以缓解该问题,但是仍然无法很好地解决,于是又提出了Compressive learning,可以将两者结合。
During the last decade, deep neural networks have become the primary backbone in many computer vision [1–4], natural language processing [5–7], or financial forecasting [8,9] systems. Nowadays, names such as ResNet [10], DenseNet [11], or BERT [6] are encountered in almost any paper in the deep learning community. Although the idea of using artificial neurons dates back to 1960s, its large scale adoption only gained momentum during the past decade. The emergence of deep neural networks started with the landmark event in 2012 when a neural network called AlexNet [12] won the ImageNet Large Scale Visual Recognition Challenge (ILSVRC) by a large margin compared to the runner up. The primary discovery from the technical report of AlexNet was that the number of hidden layers, also known as the depth of the neural network, is crucial for reaching its high performance. However, stacking more hidden layers to a neural network and optimizing the parameters of such deep networks was not an easy task due to several problems such as bad initialization, and gradient vanishing or exploding phenomena. In 2015, the proposal of skip-connection in ResNet [10], also known as residual connection, has enabled us to successfully train very deep networks with hundreds or even thousands of hidden layers. Two years later, the idea of skip-connection was extended into dense-connection in DenseNet [11], leading to a new generation of state-of-the-art networks achieving better performances while having lower complexity.
Although the error rates in ILSVRC have been gradually narrowed down over the years, it took the collective efforts of the entire research community several years to refine the manual network architectural designs and discover better design patterns improving performance.
上述段介绍了深度神经网络的发展以及目前ResNet,DenseNet,BERT,AlexNet被广泛受用。并提出了深度神经网络的逐步发展,以及各种模型的推动,使得网络模型能够获得更好的性能。
最后提出虽然网络模型在发展(ILSVRC的错误率在下降),但是整个研究过程花了很多时间在手动完善网络架构上,不过发现了更好的设计模式来提高性能。
In order to exempt practitioners from the time-consuming network architecture design process, a new area of research called Neural Architecture Search (NAS) has risen recently [13].
With neural architecture search, the focus has shifted from designing a single network architecture to designing a space of network architectures and the accompanying algorithm that searches this space to find the best architectures for a particular learning task.
The structure of the space of potential network architectures highly affects the computational complexity of a given NAS algorithm. Progressive neural network learning is a class of NAS algorithms that have highly structured search spaces: each algorithm progressively constructs the final network architecture by extending the current network topology with more neurons and neural connections at each step. For this reason, algorithms that fall into this category often have a much low training complexity compared to those operating in an unstructured search space. Besides, since candidate architectures are evaluated sequentially from having a lower complexity to higher complexity until convergence, a progressive neural network learning algorithm is capable of generating compact network architectures.
The progressive neural network learning topic will be covered in Section 9.2.
上述段提出,为了免受耗时的网络架构设计过程的影响,最近兴起了一个新的研究领域,称为NAS.
随后提出NAS的重点已经从设计单一的网络结构转移到设计一个网络结构空间和相应的算法,该算法通过搜索该空间来为特定的学习任务找到最佳的结构。
再讨论NAS的复杂度问题。顺势提出Progressive neural network learning就是一类具有高度结构化搜索空间的NAS算法,它通过在每一步扩展具有更多神经元和神经连接的当前网络拓扑来逐步构建最终的网络架构。因此,与在非结构化搜索空间中操作的算法相比,具有更低的训练复杂度。并且,提出它能够生成更紧凑的网络架构。
总之:提出NAS,再提出Progressive neural network,并提出其优点。
While neural architecture search can solve the tedious problem of designing the architecture of a neural network, deep neural networks as machine learning solutions often confront with hardware barriers when being deployed to mobile or embedded devices.
To make the deep learning paradigm more applicable and practical in real-world scenarios, effort have been dedicated to devising methodologies that can reduce the computational and memory complexities of pretrained deep neural networks. These methodologies are often referred to as model compression, which includes post-training parameter pruning [14], parameter quantization [15,16], that is, using low-precision representation for floating point numbers, low-rank approximation of the network’s parameters [17–19], or a combination of these techniques [20]. Moreover, hardware-aware run-time complexity has also been incorporated as a minimization objective in some NAS algorithms [21,22].
While significant progress has been made in these areas, solutions provided from model compression methodologies or hardware-aware NAS are mainly developed and demonstrated on highly powerful mobile devices with multiple-core processors. It is also worth noting that in many applications, such powerful and expensive units are expected to perform multiple tasks at the same time. For example, sensor data acquisition, inference about the environment and navigation are often seen as common requirements in robotics. In cases where a complete on-device processing solution is unattainable, hybrid solutions can serve as a good and practical alternative, especially in the area of Internet-of-Things (IoT). That is, some preprocessing steps are implemented on-device and intermediate data is transferred to a centralized computing server for major computation steps.
Compressive learning is a learning paradigm that can provide such a hybrid solution. In compressive learning signals are simultaneously acquired and compressed at the sensor level, and the machine learning model performs inference directly based on the compressed measurements, bypassing the signal reconstruction step.
The compressive learning topic will be covered in Section 9.3.
提出了NAS可以解决设计神经网络架构的问题,但是深度神经网络却经常面临着部署时的硬件障碍
人们致力于解决这样的障碍,想要降低训练深度神经网络计算和内存复杂性。解决这类问题的方法通常被称为model compression,它包括 训练后参数修剪、参数量化、网络参数的低秩近似 或这些技术的组合。硬件感知的运行时复杂性也被整合到了一些NAS算法中作为最小化目标。
虽然前两者方法已经有很重大的进展了,但它们目前还是在高性能设备上开发和演示的,不能在实际中解决问题,但是两者结合的混合解决方案可以作为一种很好且实用的方案(一些预处理步骤在设备上实现,中间数据被传输到中央计算服务器用于主要的计算步骤)。
Compressive learning是一种可以提供这种混合解决方案的学习范式。并介绍原理
9.2 Progressive neural network learning
Progressive Neural Network Learning (PNNL) is a class of algorithms that aim to build the network architecture in a data-driven and incremental manner until the learning performance converges.
A PNNL algorithm starts with a minimal network topology, which is often a single hidden layer network with a few hidden neurons, then it iteratively increases the learning capacity by adding new blocks of neurons to the current network topology and optimizing the corresponding new connections.
简单介绍了PNNL。
简要概括了PNNL的工作原理。
For forming new synaptic connections to the existing architecture several algorithms were proposed, each following a different expansion rule.
For example, in broad learning system [23] the network topology progression strategy only expands the width of the neural network which is restricted to have two hidden layers.
On the other hand, progressive operational perceptron [24] operates by incrementally expanding the depth of the network using a predefined maximal topology template with each layer having a fixed number of neurons.
In addition to the approaches that solely enlarge a network only in terms of width or depth, there exist more flexible algorithms such as those in [25] and [26] in which both the width and the depth of the network is progressively increased.
提出为了与现有算法增加新的突触连接,提出了很多方法,不同方法的不同点在于扩充规则不同
在broad learning system中扩展网络的宽度,限制深度(只有两个隐藏层)
在progressive operational perceptron中扩充网络的深度,限制宽度(提前给定每层固定的神经元数量)
存在更灵活的算法,即扩展网络的宽度,又扩展网络的深度
总结:介绍progression strategy
Besides the network progression strategy, different algorithms also adopt different optimization strategies. The majority of them can be divided into two main categories, namely those following a convex optimization approach and those following a stochastic gradient-based optimization approach.
For those algorithms that employ convex optimization techniques, such as the broad learning system [23] or the progressive learning network [25], randomized hidden neurons are often used and analytical solutions are only derived for the output layer.
Nowadays, with the increasing availability of large datasets and affordable computing hardware, stochastic gradient-based optimization has also been a popular choice for building progressively neural networks [24,26,27]. Compared to the convex optimization approach, employing stochastic gradient-based optimization is less memory-intensive, however, at the cost of longer training times. Since algorithms that employ convex optimization also utilize randomized neurons, the final network architectures obtained by such algorithms are often larger than those generated by algorithms based on stochastic gradient-based optimization.
There are also algorithms that combine both optimization techniques, such as the heterogeneous multilayer generalized operational perceptron [26], which takes advantage of convex optimization and randomized neurons to speed up its architecture evaluation procedure and stochastic gradient descent to finetune the best candidate architectures. This combination does not only enable efficient training, but also the finding of compact network architectures.
提出optimization strategy主要被分为两类
- following a convex optimization approach(基于凸优化方法)
following a stochastic gradient-based optimization approach(基于随机梯度优化方法)
介绍采用凸优化方法的算法,经常使用随机隐藏神经元并且仅导出输出层的解析解
提出采用随机梯度优化方法的算法也称为热门选择。并与凸优化方法进行比较,其占用内存较少,获得的网络结构更小,但训练时长较长。
提出也有算法结合了前两类,利用凸优化和随机神经元家开架构评估过程,并利用随机梯度下降来微调最佳候选架构。这种组合可以实现高效训练,且得到的网络架构也更紧凑(更小)
In the next sections, we will present two representative algorithms that utilize convex optimization and randomization, namely the broad learning system [23] in Section 9.2.1 and the progressive learning network [25] in Section 9.2.2.
Then we will cover representative algorithms that adopt stochastic gradient-based optimization, namely the progressive operational perceptron and its variants in Section 9.2.3.
In Section 9.2.4, we will cover the heterogeneous multilayer generalized operational perceptron algorithm that takes advantage of both optimization approaches.
Finally, in Section 9.2.5, we will cover a method that was proposed to speed up and enhance the progressive learning procedure.
介绍了接下来的五个小节的主要内容。
9.2.1和9.2.2介绍关于凸优化方法的代表算法
9.2.3介绍关于随机梯度优化方法的代表算法及其变体
9.2.4介绍结合两种优化方法的代表算法
9.2.5介绍加快和增强渐进式学习过程的方法
9.2.1 Broad learning system
Broad Learning System (BLS) is a two-hidden layer network architecture, which is a generalization of the random vector functional link neural network [28,29]. Given a training set of $N$ samples, let us denote the inputs and the labels as $X \in \mathbb{R}^{N \times D{in}}$ and $Y \in \mathbb{R}^{N \times D{out}}$ , respectively.
简要介绍BLS,并给出通用符号定义
The first hidden layer, also called the feature layer, is formed by the concatenation of feature nodes.
Feature nodes represent nonlinear features extracted from the input via the following transformation:
where $\boldsymbol{Z}i \in \mathbb{R}^{N \times D{fi}}$ denotes the output of the $i$th feature node, $\boldsymbol{W}{fi} \in \mathbb{R}^{D{in} \times D{fi}}$ denotes the random weights and $\boldsymbol{B}{fi} \in \mathbb{R}^{1\times D_{fi}}$ denotes the bias term and $\boldsymbol{1}_N \in \mathbb{R}^N$ denotes a constant vector of ones, and $\phi(\cdot)$ is a nonlinear elementwise activation functin such as the sigmoid or the Rectified linear Unit (ReLU) functions.
Multiple feature nodes can be used for the first hidden layer, and the concatenation of $n$ feature nodes is denoted by $\boldsymbol{Z}^{(n)} = [\boldsymbol{Z}1, \boldsymbol{Z}_2, \cdots , \boldsymbol{Z}_n] \in \mathbb{R}^{N \times (D{f1} + \cdots +D_{fn})}$.
Here, we use $[\boldsymbol{A}, \boldsymbol{B}]$ to express the horizontal concatenation of matrices $\boldsymbol{A} \in \mathbb{R}^{P \times Q_1}$ and $\boldsymbol{B} \in \mathbb{R}^{P \times Q_2}$ , resulting in a matrix of size $P \times (Q_1 + Q_2)$.
提出第一个隐藏层为特征层,是由特征节点串联组成的(引出特征节点)
给出了变换公式,特征节点表示从该变换中提出的非线性特征(解释特征节点)
The second hidden layer, also known as the enhancement layer, is formed by the concatenation of enhancement nodes.
Enhancement nodes represent highly nonlinear features, which are extracted from the feature nodes $\boldsymbol{Z}^{(n)}$ via the following transformation:
where $\boldsymbol{H}j \in \mathbb{R}^{N \times D{ej}}$ denotes the output of the $j$th enhancement node, $\boldsymbol{W}{ej} \in \mathbb{R}^{(D{f1} + \cdots + D{fn}) \times D{ej}}$ denotes the random weights connecting all feature nodes and the $j$th enhancement node and $\boldsymbol{B}{ej} \in \mathbb{R}^{1 \times D{e_j}}$ denotes the corresponding bias term and $\boldsymbol{1}_N$ denotes a constant vector of ones, and $\zeta(\cdot)$ is a nonlinear element-wise activation function, such as sigmoid or rectified linear unit (ReLU).
The choice of $\phi(\cdot)$ and $\zeta(\cdot)$ is determined by the user.
提出第二个隐藏层为增强层,有增强节点串联组成(引出增强节点)
给出了变换公式,增强节点表示高度非线性的特征,这些特征是从特征节点$\boldsymbol{Z}^{(n)}$(特征节点如上段内容)中通过该变换公式提取出的(解释增强节点)
最后提出对于特征节点和增强节点公式中的非线性函数都是用户可选的
BLS generates predictions by learning a linear classifier or regressor based on the feature nodes and enhancement nodes. Specifically, the predictions generated by a BLS network are computed as follows:
where $\boldsymbol{H}^{(m)} = [\boldsymbol{H}1, \boldsymbol{H}_2, \cdots , \boldsymbol{H}_m] \in \mathbb{R}^{N ×(D{e1} +\cdots+D{em} )}$ denotes the concatenation of $m$ enhancement nodes; $\boldsymbol{W}^m_n \in \mathbb{R}^{(D{f1} + \cdots + D{fn} + D{e1} + \cdots + D{em} ) \times D{out}}$ denotes the output weight matrix that connects the output nodes with the $n$ feature nodes and $m$ enhancement nodes.
上述给出BLS生成的预测计算公式。
其中的$\boldsymbol{Z}^{(n)}$是feature nodes,$\boldsymbol{H}^{(m)}$是enhancement nodes,$\boldsymbol{W}_n^m$是权重参数
An illustration of the BLS model is shown in Fig. 9.1. This network formulation is widely adopted in the follow-up works that extend the BLS model, for example, [30,31]. However, we should note that in the original work, the authors also described another formulation variant, which is called BLS with alternative enhancement node construction, which is shown in Fig. 9.2.
As can be seen from Figs. 9.1 and 9.2, the only difference between the two formulations is on how an enhancement node is computed. In the standard formulation described in Eq. (2), each enhancement node is connected to all feature nodes while in the alternative construction, one enhancement node is connected to a corresponding feature node.
As a result, the number of feature nodes and enhancement nodes must be the same in the alternative formulation. When this property holds for the standard formulation, under certain assumptions, the authors in [23] have proven that the two formulations are equivalent.
For the rest of this section, we will cover the standard BLS formulation. Interested readers can consult the original article [23] for further details regarding the alternative formulation.
上述给出Broad learning system以及其变体的计算公式
两者的不同点在于enhancement nodes的计算方式
对于alternative formulation要求feature nodes和feature nodes的维度需要相同。当这个性质可以用于标准公式时,这两个公式是等价的。
接下来都主要角色标准的BLS公式
Since BLS is a progressive learning model, the optimization procedure consists of two steps:
- optimizing the initial network topology
- progressive network expansion until convergence.
BLS belongs to the class of models that utilize randomization and convex optimization technique. During both the initial network optimization phase and the progressive expansion phase, BLS assigns random weights drawn from a uniform distribution to the feature nodes and the enhancement nodes, and only provides analytical solution for the output weights.
Given an initial network topology having $n$ feature nodes and $m$ enhancement nodes, the solution of the output weight matrix is calculated by solving the least-squares objective and is given by
where $(\cdot)^\dagger$ denotes the pseudo-inverse operator.
给出BLS模型的优化过程(两个步骤)
解释BLS的初始化(利用随机化和凸优化技术)和输出特点(只提供输出权重的解析解)
最终给出输出权重矩阵的计算公式(利用最小二乘法解)
After determining the parameters of the initial network architecture, there are two options to expand this network, namely adding new feature nodes or adding new enhancement nodes.
Without the loss of generality, we consider the case when one enhancement node having a dimension of $D{e{m+1}}$ is added to the initial network topology.
This expansion step leads to the addition of the weight matrix $\boldsymbol{W}{e{m+1}} \in \mathbb{R}^{(D{f1} + \cdots + D{fn}) \times D{em+1}}$, connecting $n$ feature nodes to the new enhancement node. The values of $\boldsymbol{W}{e{m+1}}$ are again obtained by randomly sampling from a uniform distribution. In addition to $\boldsymbol{W}{e{m+1}}$ , the expansion of a new enhancement node also leads to the expansion of the output weight matrix from $\boldsymbol{W}^m_n \in \mathbb{R}^{(D{f1} + \cdots + D{fn} + D{e1} + \cdots + D{em}) \times D{out}}$ to $\boldsymbol{W}^{m+1}n \in \mathbb{R}^{(D{f1} + \cdots + D{fn} + D{e1} + \cdots +D{em+1}) \times D{out}}$ . Following Eq. (4), the values of $W^{m+1}_n$ can be computed as follows:
where $\boldsymbol{H}^{(m+1)} = [\boldsymbol{H}^{(m)}, \boldsymbol{H}_{m+1}]$.
在确定初始网络架构的参数后,有两个选择来扩展网络
- 添加新的feature nodes
添加新的enhancement nodes
一般考虑将一个维度为$D{e{m+1}}$(比原维度大一维)的enhancement node添加到初始网络的拓扑结构中
添加节点后会导致权重矩阵扩充,并给出了扩充公式
We define $\boldsymbol{A}^m_n = [\boldsymbol{Z}^{(n)}, \boldsymbol{H}^{(m)}]$ and $\boldsymbol{A}^{m+1}_n = [\boldsymbol{Z}^{(n)}, \boldsymbol{H}^{(m+1)}]$. A straightforward way to compute the pseudo-inverse of $\boldsymbol{A}^{m+1}_n$ is to perform singular value decomposition on $\boldsymbol{A}^{m+1}_n$.
However, as the number of enhancement nodes increases, repeating this step leads to a significant amount of computation. In order to reduce the computational complexity when computing the pseudoinverse of $\boldsymbol{A}^{m+1}_n$, BLS adopts an incremental approach to compute $(\boldsymbol{A}^{m+1}_n)^\dagger$ based on $(\boldsymbol{A}^m_n)^\dagger$ as follows:
where $\boldsymbol{D} = (\boldsymbol{A}^mn)^\dagger\boldsymbol{H}{m+1}$ and
with $\boldsymbol{C} = \boldsymbol{H}^{m+1} − \boldsymbol{A}^m_n \boldsymbol{D}$. Combining Eq. (5) and Eq. (6) leads to the following equation that can be used to calculate the new output weight matrix $\boldsymbol{W}^{m+1}_n$ based on the initial output weight matrix $\boldsymbol{W}^m_n$:
定义$\boldsymbol{A}_n^m$和$\boldsymbol{A}_n^{m+1}$,并提出计算$\boldsymbol{A}^{m+1}_n$ 的伪逆矩阵的方式为直接对其求奇异值分解
但是随着enhancement nodes数量增加,计算的复杂度很高。为了降低复杂度,BLS提出了如Eq. (6) 的增加方法。并给出计算方法
A similar approach can also be derived for incrementally updating the output weight matrix when new feature nodes are added.
Specifically, let us consider the case when one feature node $(\boldsymbol{Z}_{n+1})$ is added to the current network architecture of $n$ feature nodes and $m$ enhancement node. This new feature node leads to the generation of the following enhancement nodes:
where $\boldsymbol{W}{ex_1}, \dots, \boldsymbol{W}{exm}, \boldsymbol{B}{ex1}, \dots, \boldsymbol{B}{ex_m}$ are randomly generated.
可以导出类似的方法用于在添加新特征节点时增量更新输出权重矩阵
并给出了新增特征节点更新增强节点的公式
The output layer now not only takes $\boldsymbol{A}^mn$ as inputs but also $\boldsymbol{Z}{n+1}$ and $\boldsymbol{H}{ex_m}$. That is, $\boldsymbol{A}^m{n+1} = [\boldsymbol{A}^mn, \boldsymbol{Z}{n+1}, \boldsymbol{H}{ex_m}]$. The update equation for $(\boldsymbol{A}^m{n+1})^\dagger$ based on $(\boldsymbol{A}^m_n)^\dagger$ is the following:
where $\boldsymbol{D} = (\boldsymbol{A}^mn)^\dagger[\boldsymbol{Z}{n+1}, \boldsymbol{H}_{ex_m}]$ and
with $\boldsymbol{C} = [\boldsymbol{Z}{n+1}, \boldsymbol{H}{ex_m}] - \boldsymbol{A}_n^m\boldsymbol{D}$.
给出了从$(\boldsymbol{A}^mn)^\dagger$更新为$(\boldsymbol{A}^m{n+1})^\dagger$的公式
While providing a fast solution to update the parameters of the network when new enhancement nodes or feature nodes are added, no particular progression strategy is proposed in [23]. Since the enhancement nodes take the feature nodes as inputs, we empirically found that adding the feature nodes until convergence before adding the enhancement nodes is a good progression strategy for the BLS model. Besides, the empirical results in [23] suggest that the total dimension of the enhancement nodes or the feature nodes should be on the order of thousands in order to obtain good performance.
在添加增强节点之前添加特征节点直到收敛是BLS模型的一个很好的progression strategy。
增强节点或特征节点的总维数为数千量级可以获得更好的性能
9.2.2 Progressive learning network
Progressive Learning Network (PLN) [25] is also an algorithm that adopts convex optimization and randomization approaches. Different from broad learning system, the progression strategy in PLN allows us to construct multilayer fully-connected networks, instead of only two hidden layers as in BLS.
More specifically, the progression strategy in PLN constructs the network architecture in a layer-by-layer manner until convergence, starting from an one hidden layer network. Each hidden layer in PLN comprises of both deterministic and randomized neurons. The weight values of deterministic neurons are computed by solving a linear optimization problem while the weight values of the randomized neurons are computed by sampling from a random uniform distribution.
To construct a new hidden layer, the algorithm first computes the deterministic neurons, and then incrementally adds neurons with random parameters until the learning performance saturates.
介绍PLN的特点(采用凸优化和随机化方法),与BLS对比提出PLN通过构造多层全连接层(变深)
介绍PLN的学习过程(先开始与一层隐藏层,逐层学习,逐层变深,每个隐藏层都含有确定性和随机性神经元,确定性神经元的权重通过计算线性优化问题的解得出,随机性神经元的权重通过从随机均匀分布中采样计算得出)
介绍PLN构造新的隐藏层的处理办法(先计算确定性神经元,再计算随机性神经元,直到性能饱和)
To demonstrate how a hidden layer is optimized in the PLN model, we assume that the current network architecture has $k$ hidden layers and the PLN algorithm proceeds by adding the $(k + 1)$-th hidden layer to the current network architecture.
At this step, the weights of the previous $k$ hidden layers are fixed and the PLN algorithm only optimizes the $(k + 1)$-th hidden layer as well as the output layer.
We illustrate a $(k + 1)$-hidden layer PLN network in Fig. 9.3.
给出符号定义
解释前$k$个隐藏层是固定的,只优化第$k+1$个隐藏层
Let us denote the $i$th sample and its target vector by $\boldsymbol{x}_i \in \mathbb{R}^P$ and $\boldsymbol{y}_i \in \mathbb{R}^Q$, respectively. In addition, given $\boldsymbol{x}_i$ as the input to the network, let us denote $\boldsymbol{x}^{(k)}_i \in \mathbb{R}^{P_k}$ as the output of the $k$th hidden layer. As mentioned previously, a hidden layer in PLN consists of both deterministic neurons and randomized neurons. Thus $\boldsymbol{x}^{(k+1)}_i$ is formed by the concatenation of deterministic and randomized neurons as follows:
where $\boldsymbol{d}_i^{(k+1)}$ and $\boldsymbol{r}_i^{(k+1)}$ denote the outputs of deterministic and randomized neurons of the $(k+1)$-th hidden layer, respectively. $\phi(\cdot)$ is an elementwise activation function that satisfies the Progression Property (PP).
According to [25], an elementwise nonlinear function $\phi(\cdot)$ holds progression property if there are two known linear transformations $\boldsymbol{V}_N \in \mathbb{R}^{M \times N}$ and $\boldsymbol{U}_N \in \mathbb{R}^{N \times M}$ such that $\boldsymbol{U}_N \phi(\boldsymbol{V}_N \boldsymbol{x}) = \boldsymbol{x}, \forall \boldsymbol{x} \in \mathbb{R}^N$.
It can be easily verified that the PP holds for ReLU activation function by setting:
where $\boldsymbol{I}_N$ is the identity matrix of $N$ samples.
给出第$k+1$层的第$i$个样本的输出的表达式
解释根据[25]可以得出:两个已知线性变换使得$\boldsymbol{U}_N \phi(\boldsymbol{V}_N \boldsymbol{x}) = \boldsymbol{x}, \forall \boldsymbol{x} \in \mathbb{R}^N$成立则非线性函数$\phi(\cdot)$满足Progression property。
很容易验证对ReLU激活函数进行上述设置可以满足Progression property
The deterministic neurons are computed using the following relation:
where $\boldsymbol{V}Q$ is the PP holding matrix as defined in Eq. (13). $\boldsymbol{W}^∗{k+1}$ is obtained by solving the regularized least-squares optimization problem:
where $\lambda$ is a predefined regularization coefficient.
给出确定性神经元的计算公式
The randomized neurons are generated by applying a linear transformation:
where $\boldsymbol{R}_{k+1}$ is a random matrix with values drawn from a uiniform distribution.
给出随机性神经元的计算公式
As we can see from Eq. (14), for any hidden layer, the dimension of the deterministic neurons is always $2Q$, which is twice the number of dimensions of the target vectors. The dimension of the randomized neurons is progressively increased until the learning performance converges.
解释每个隐藏层中确定性神经元和随机性神经元的维度数量特点
Given the output of the $(k + 1)$-th hidden layer $\boldsymbol{x}^{(k+1)}_i$, the PLN model makes prediction by learning a linear classifier/regressor that minimizes the reconstruction error:
where $\alpha$ is a predefined regularization coefficient and $\boldsymbol{U}_Q$ is the PP holding property matrix defined in Eq. (13).
The optimization problem in Eq. (17) is a convex optimization problem, which can be solved by existing convex solvers, like the Alternating Direction Method of Multipliers (ADMM) [32].
给出PLN模型的学习方法(通过学习最小化重构误差的线性分类器/回归器进行预测)
9.2.3 Progressive operational perceptron and its variants
本章在解释POP前,先解释了POP的核心组件GOP(一种神经元,执行三个操作:nodal、pooling、activation)。
然后介绍POP以及其求解方法(two-pass GIS)。
之后介绍POPfast和POPmen(POPfast是POP的变体,比POP更快,POPmem是POP的变体,更能考虑到空间信息)
Progressive Operational Perceptron [24] (POP) is an algorithm that heavily takes advantage of the gradient-based optimization to not only learn the network topology but also the assignment of different nonlinear transformations to different layers following a data-driven process.
Before diving into the details of the progression strategy and the optimization routine in POP, it is important to become familiar with a generalized neuron model that serves as a core component in POP, as well as in other PNNL algorithms that we will cover next in this chapter.
介绍POP算法的特点和优点(充分利用基于梯度的优化、可以学习网络拓扑,可以再数据驱动过程之后为不同的层分配不同的非线性变换)
先熟悉作为POP核心组件的广义神经元模型(就是GOP)是很重要的
The neuron model is a critical component that defines the modeling ability of a neural network. The most common neuron model used nowadays is based on the design of McCulloch–Pitts perceptron [33] (hereafter simply referred to as perceptron), which performs a linear transformation followed by a nonlinear activation function.
There have been several attempts [34–36] to design novel neuron models that can better capture the nonlinear relationships often existing between the inputs and the targets. Generalized Operational Perceptron (GOP) [24] is such a neuron model that can express a wide range of nonlinear transformations, including the one modeled by the perceptron. GOP is designed to better simulate biological neurons in the mammalian nervous system.
Specifically, a GOP performs three distinct operations, namely the nodal, the pooling and the activation operations that correspond to the operations observed in a biological neuron.
介绍目前最常见的神经元模型(先执行线性变换,然后执行非线性激活函数)
介绍GOP感知器模型(该模型可以更好地(相比于McCulloch-Pitts perceptron)捕捉输入和目标之间经常存在的非线性关系,它可以表达广泛的非线性变换,包括感知器建模的非线性变换)
GOP会执行节点操作、池化操作和激活操作
Let us consider the $i$th GOP of the $k$th layer in a fully-connected GOP network. A GOP takes a vector as input, which represents the output vector of the previous layer, and outputs a scalar. In the following, we use the notation $x^{(k−1)}j \in \mathbb{R}\ \text{for}\ j =1,\dots , N{k−1}$ to denote the $j$th output of the $(k − 1)$-th layer. Thus the output of the GOP under consideration is denoted by $x^{(k)}_i \in \mathbb{R}$.
The first operation performed by a GOP is the nodal operation, which modifies each individual output of the previous layer using a synaptic weight:
where $\psii^{(k)}(\cdot)$ is the nodal operator of the $i$th GOP in the $k$th layer; $x_j^{(k-1)} \in \mathbb{R}$ is the $j$th output of the $(k-1)$th layer, and $w{ji}^{(k)} \in \mathbb{R}$ is the synaptic weight connecting the $j$th neuron of the $(k-1)$th layer to the $i$th neuron of the $k$th layer.
The second operation performed by a GOP is the pooling operation, which summarizes the modified input signals generated by the nodal operation into a scalar:
where $\rho^{(k)}i (\cdot)$ denotes the pooling operator, and $z^{(k)}{ji}, j = 1, \dots , N_{k−1}$ denote the outputs of the nodal operation in Eq. (20). $b^{(k)}_i \in \mathbb{R}$ denotes the learnable bias term, which is used to offset the pooled result.
Similar to other neuron models, the final operation of a GOP is the activation operation:
where $f^{(k)}_i (\cdot)$ denotes the activation operator and $t^{(k)}_i$ denotes the output of the pooling operation.
给出符号定义
给出第一个操作(nodal operation)的更新公式
给出第二个操作(pooling operation)的更新公式
给出第三个操作(activation operation)的更新公式
Fig. 9.4 illustrates the working mechanism of generalized operational perceptron. As can be seen from this figure, a GOP is characterized by the set of synaptic weights including the bias and the set of operators (nodal, pooling and activation).
The functional form of an operator is selected, usually through optimization, from a library of predefined functions such as the ones provided in Table 9.1.
Hereafter, we use the term operator set to refer to a specific choice of one nodal, one pooling and one activation operators. Each GOP is equipped with an operator set, which can be different from the operator sets of other GOPs.
在图中说明了GOP的工作机制,可以看出GOP的特征是突触权重集合,包括偏置和操作集合(nodal,pooling,activation)
提出操作集合是可选择的,并在表中给出了可选项。
规定下文的术语
Although the abstraction through operator set in GOP allows a higher degree of flexibility and diversity, optimizing neural networks that are formed by GOPs is a challenging problem since we need to optimize not only the synaptic weights but also the assignment of operator set to each specific GOP.
Given a predefined library of $L$ operator sets and a GOP network of $M$ neurons, there are $L^M$ different ways to make the operator set assignment, corresponding to $L^M$ different neural networks having different functional forms. That is, the space of nonlinear functions encapsulated by a GOP network scales exponentially with respect to the number of neurons.
先提出GOP方法的缺点:优化由GOP组成的神经网络是一个具有挑战性的问题,因为不仅需要优化突触权重,还需要优化操作符集合到每个特定GOP的分配
具体解释GOP网络封装的非线性函数空间相对于神经元的数量呈指数增长
Progressive operational perceptron is an algorithm that trains an instantiation of GOP networks in a layer-by-layer manner, given a predefined network template, which specifies the maximum number of layers and the number of GOPs in each layer.
To make the optimization problem computationally tractable, POP assigns the same operator set to all GOPs within the same layer. This constraint significantly reduces the number of candidate assignments, which are evaluated by a gradient descent-based optimization process.
先介绍POP算法,它在给定预定义的网络模版的情况下,以逐层方式训练GOP网络的实力化,它指定网络最大层数和每层的GOPs数量
未来解决上述的GOP网络封装的非线性函数空间对神经元的数量呈指数增长,POP统一了同一层内的所有GOPs的运算集
Specifically, given a target loss value $\alpha$ and a maximal network template of $k$ hidden layers $T = [D{in}, N_1, \dots , N_K , D{out}]$ with the $k$th hidden layer having $N_k$ GOPs, POP iteratively learns one hidden layer at each step and terminates when the target loss value is achieved or all hidden layers have been learned.
At the $k$th step, POP forms a neural network with $k$ hidden layers having the following network template $Tk = [D{in}, N1, \dots , N_k , D{out}]$. At this point, all previous $k − 1$ hidden layers have been optimized and fixed. Since all GOPs within a layer share the same operator set, the optimization problem at the $k$th step is to find the best operator set assignment and the weight values for the $k$th hidden layer and the output layer.
POP tackles this problem by evaluating a reduced set of possible assignments via a two-pass Greedy Iterative Search (GIS) procedure.
给出符号定义,解释POP在每一步迭代地学习一个隐藏层,并在实现目标损失值或学习所有隐藏层时终止
提出前$k-1$层的GOPs已经训练好了,训练第$k$层的GOPs的主要问题是设置操作集以及找到隐藏层和输出层的权重值
POP通过两遍贪婪迭代搜索(GIS)程来评估一个简化的可能赋值集,从而解决了这个问题。
Let $\phi_k$ and $\phi_o$ be the operator sets of the $k$th hidden layer and output layer, respectively.
In the first pass of GIS, $\phi_k$ is selected randomly from the operator library and the best performing $\phi^∗_o$ is chosen by evaluating all possible operator sets. That is, for every operator set that is assigned to $\phi_o$ we randomly initialize the weights of thekth hidden layer and the output layer and train the network instance for $E$ epochs. Once $\phi^∗_o$ is found, the algorithm continues by fixing $\phi^∗_o$ and optimizing $\phi^∗_k$ through the same evaluation procedure, that is, now the selected $\phi^∗_o$ is used and the best operator set $\phi^∗_k$ is found by using all operator sets.
All the steps conducted in the first pass are repeated for the second pass of GIS, except the selection of the initial $\phi_k$, which is set to the one selected by the first pass of GIS.
先给出符号定义
介绍GIS的两个步骤
- 第一步:随机从操作集中选择$\phi_k$,并通过评估所有可能的操作集选择性能最好的$\phi^_o$,选择好了$\phi^_o$之后,使用该$\phi^_o$再找到最佳$\phi^_k$
- 第二步:重复第一步,但$\phi_k$直接使用第一步的$\phi_k$
After determining best operator sets for the kth hidden layer and the output layer through the two-pass GIS, the assignment $\phi^∗_k$ and the synaptic weights of the $k$th hidden layer are fixed.
The algorithm continues to build the next hidden layer from the maximal network template if the current loss value is larger than the predefined target value $\alpha$, otherwise it terminates the process.
In the first case the output layer is discarded and a new hidden and output layers are learned, while in the latter case the learned output layer is kept and the final network architecture is formed by all the hidden layers determined by the successive GIS optimization processes and the output layer of the final last layer.
在通过两遍GIS确定第$k$个隐藏层和输出层的最佳算子集后,固定了第$k$个隐层的赋值$\phi^*_k$和突触权重。
给出网络的终止条件(当前损失值小于预定义的目标值)
如果网络继续学习,则放弃输出层,学习新的隐藏层和输出层;如果终止学习,则保留学习到的输出层,并且由确定的所有隐藏层和最后一层的输出层形成最终的网络架构
Using the network construction strategy of POP, there are $P^2$ different ways to assign the operator set for the $k$th hidden layer and the output layer at step $k$, resulting in $P^2$ different network candidates for evaluation. Based on the two-pass GIS procedure, optimizing a hidden layer in POP requires four iterations over all operator set choices, which only evaluates $4P$ candidate assignments. Although this approach reduces the computational complexity significantly, it is suboptimal since only a small subset of the search space is evaluated.
给出POP方法和two-pass GIS方法的复杂度
- POP:$P^2$
- two-pass GIS:$4P$
two-pass GIS明显降低了复杂度
In order to speed up and enhance the optimization procedure in POP, a faster variant of POP called POPfast was proposed in [27]. The key idea in POPfast that enables improvements over POP in computational complexity is the relaxation of the output layer as a linear layer followed by an appropriate activation function, that is, the softmax function for classification problems and the identity function for regression problems. This relaxation reduces the search space from having $P^2$ to $P$ candidate candidates when learning a new hidden layer. This is because with the relaxation, we no longer need to optimize the operator set of a hidden layer in conjunction with that of the output layer.
At the $k$th step, POPfast constructs a $k$ hidden layer network similar to POP. The algorithm finds the best performing operator set $\phi^∗_k$ for the $k$th hidden layer by iterating through all operator sets. For each candidate operator set, it randomly initializes the weight values of the kth hidden layer and the output layer, and it optimizes them for few epochs.
Compared to POP, POPfast only requires one iteration (versus four in POP) over all the operator set while evaluating the entire search space (versus a small subset of search space as in POP).
根据POP提出一种计算速度更快的变体POPfast,并解释计算复杂度更好的原因(将松弛的输出层作为跟随着适当的激活函数的线性层),因为这种松弛会将搜索空间从$P^2$个候选对象减少到$P$个,并且不需要将隐藏层的操作集与输出层的操作集一起优化
具体解释POPfast的原理:构造一个类似于POP的第$k$个隐藏层网络,遍历所有的操作集来寻找该隐藏层的最佳操作集$\phi_k^*$,对于每个候选操作集,它随机初始化第$k$个隐藏层和输出层的权重,并经过多个epoch进行优化
比较POP和POPfast的计算次数,表明POPfast比POP好
A memory augmented variant of POPfast, known as POPmem, is proposed in [27], which builds the network architecture so that the output layer and the newly constructed hidden layer have direct access to lower-level features extracted by previous layers. This direct access is enabled via memory paths, which are informationpreserving linear transformations.
基于POPfast提出一种内存增强变体POPmem。解释POPmem的原理:使输出层和新构建的隐藏层可以访问由前一层提取的较低级别(更靠前的层)的特征,这种直接访问是通过内存路径实现的,内存路径是保留信息的线性转换
Let $\boldsymbol{x}^{(k−1)}$ be the input to the $k$th hidden layer, with $\boldsymbol{x}^{(0)}$ being the input data (the input to the network). In addition, let us denote the transformation performed by the GOPs in the $k$th hidden layer as $\mathcal{F}_k$ . The $k$th hidden layer only observes $\boldsymbol{x}^{(k−1)}$ as its input and does not have direct access to $\boldsymbol{x}^{(k−2)} , \boldsymbol{x}^{(k−3)} , \dots, \boldsymbol{x}^{(0)}$, which are the shallower features extracted by the previous hidden layers and the input. Similarly, the output layer only observes $\mathcal{F}_k(\boldsymbol{x}^{(k−1)})$ as its input and does not have direct access to information from previous hidden layers.
POPmem provides a remedy for this problem by incorporating a memory path in parallel to the $k$th hidden layer formed by GOPs.
Let us denote by $\mathcal{G}$ a linear projection that preserves information of the input data. The type of information retained depends on how the weight matrix of $\mathcal{G}$ is obtained. For example, using Principal Component Analysis (PCA) $\mathcal{G}$ can preserve the energy of the input data while using Linear Discriminant Analysis (LDA) $\mathcal{G}$ can preserve the linear class separability between different classes.
给出后续的符号定义,主要是第$k$层的输入,和第$k$层进行的变换(函数)。最后提出第$k$个隐藏层和输出层都只能从前一层的隐藏层和输入提取特征(这样提取的特征就很浅)
提出POPmen解决上述问题的方法:将存储器路径和GOP的第$k$个隐藏层进行并行结合
提出符号定义$\mathcal{G}$表示保留输入数据信息的线性投影。保留的信息类型取决于GIS的权重矩阵是如何获得的
At the $k$th step, POPmem constructs a $k$ hidden layer network. The $k$th hidden layer is formed by concatenating $Nk$ GOPs, that is, $\mathcal{F}^{(k)} (\boldsymbol{x}^{(k−1)} )$ and the information preserved from the $(k − 1)$-th hidden layer, that is, $\mathcal{G}^{(k)} (\boldsymbol{x}^{(k−1)} )$. $\mathcal{G}^{(k)}$ denotes the memory path of the $k$th hidden layer, which is estimated from $\boldsymbol{x}^{(k−1)}_i$ , with $i$ denoting the index of the training sample. For example, to preserve the energy of the data,$\mathcal{G}^{(k)} (\boldsymbol{x}) = \boldsymbol{W}^T{\mathcal{G}_k} \boldsymbol{x}^{(k−1)}$ is obtained by solving the signal reconstruction problem:
where $\boldsymbol{W}^T$ denotes the transpose of $\boldsymbol{W}$ and $\boldsymbol{I}$ denotes the identity matrix of appropriate size.
具体提出符号表示,并且提出$\mathcal{G}^{(k)}(\boldsymbol{x})$的表达式,其中包含权重信息$\boldsymbol{W}^T{\mathcal{G}_k}\boldsymbol{x}^{(k-1)}$,并给出$\boldsymbol{W}{\mathcal{G}_k}$的求解公式
By construction, we have the following recursive relation in the network architectures that are learned by POPmem:
Here we should note that at the kth step in POPmem, $\mathcal{G}^{(k)}$ is determined by solving the corresponding optimization problem that defines the information-preserving property. After that, the parameters of $\mathcal{G}^{(k)}$, that is, $\boldsymbol{W}_{\mathcal{G}_k}$ , are fixed during the optimization of $\mathcal{F}^{(k)}$. In POPmem, the GOPs of the $k$th hidden layer $(\mathcal{F}^{(k)})$ and the output layer are optimized in the same manner as in POPfast. In Fig. 9.5, we illustrate the network construction until the third hidden layer by POPmem.
利用图的形式解释POPmen的工作原理
For POP and its variants, once the final network architecture has been determined, the parameters of the entire network can be further finetuned using stochastic gradient descent with a small learning rate.
总结POP和它的变体,一旦确定了最终的网络架构,就可以使用具有小学习率的随机梯度下降来进一步微调整个网络的参数
9.2.4 Heterogeneous multilayer generalized operational perceptron
As we have seen from the previous section, POP and its variants tackle the exponential search space in GOP networks by imposing a homogeneity constraint, that is, GOPs within a layer share the same operator set assignment. Although this decision reduces the computational complexity when evaluating operator sets and constructing the network architecture using stochastic gradient descent algorithm, it significantly reduces the space of potential network architectures. In addition, using POP and its variants, the design of the final network architecture is only semiautomatic since the users still need to define the maximum number of layers and the number of neurons for each layer.
Heterogeneous Multilayer Generalized Operational Perceptron (HeMLGOP) [26] overcomes the aforementioned limitations in POP and its variants. Similar to BLS and PLN algorithms that have been covered in Sections 9.2.1 and 9.2.2, respectively, HeMLGOP also takes advantage of randomization and convex optimization to speedily evaluate the operator set assignment. This addresses the computational bottleneck encountered in POP and its variants when evaluating potential operator sets. Besides, HeMLGOP increases heterogeneity characteristic into the learned network architecture by allowing different GOPs within the same hidden layer to have different operator sets, enabling the neural network under construction the capability to model a wider range of functions. Finally, HeMLGOP is an algorithm that learns a neural network architecture in a fully automatic manner, being capable of constructing network architectures of any width and depth size in a data-driven manner, depending on the difficulty of the problem at hand.
总结POP及其变体的原理(对GOP施加同质性约束(同一层的操作集相同)来避免指数搜索空间)。然后讨论POP方法的缺点:该方法虽然降低了构建网络架构时的计算复杂度,但它显著减少了潜在网络架构的空间。并且最终网络体系的设计是半自动的(需要用户定义最大层数和每一层的神经元数量)
介绍HeMLGOP(异构多层广义运算感知器,异构多层GOP):
Fig. 9.6 illustrates the progression strategy adopted by HeMLGOP. The algorithm builds the network architecture in a block-by-block manner, with $S_b $ being the number of neurons of a block, given as a hyperparameter.
At the first step, HeMLGOP forms a single hidden layer network with one block of GOPs. Once this block of neurons is optimized in conjunction with the output layer, the algorithm moves to the next step.
At each step, the algorithm expands the current network architecture by adding a new block of neurons to the last hidden layer, hereafter also referred to as the current hidden layer. A hidden layer continues to expand until the performance obtained is saturated, which is measured by checking the rate of improvement:
where $\epsilon$ is a predefined threshold, and $vi$ denotes the loss value obtained at step $i$. Here, we assume that $\mathcal{N}{i−1}$ and $\mathcal{N}_i$ have the same number of hidden layers, with Nidenoting the network architecture obtained at step $i$. That is, at the end of the $i$-th step, if the relation in Eq. (23) does not hold, the progression in the current hidden layer continues. Otherwise, the new block of neurons that is added at step $i$ is removed from the network architecture.
This is because the addition of this new block only leads to a marginal relative performance improvement (less than a given threshold $\epsilon$). In this scenario, HeMLGOP further evaluates whether a new hidden layer should be formed or the algorithm should terminate by evaluating the following relation:
where $j$ denotes the step index such that $Dj = D_i − 1$ and $D{j+1} = Di$ , with $D_i$ denoting the number of hidden layers of the network architecture obtained at the end of step $i$. Here, we use the loss value $v{i−1}$ representing the performance of the current architecture because the new block of neurons added at step $i$ has been removed. $\zeta$ is a predefined threshold value to control the progression between layers.
先给出HeMLGOP的渐进式策略,如图所示。根据图片可以看出HeMLGOP的策略是先判断当前层是否需要添加神经元(GOP)(提前设置一个超参数$\epsilon$,根据Eq .(23)判断是否添加);再判断是否添加一个隐藏层(根据Eq .(24)判断)。如果都不添加则输出最终架构。
If the relation in Eq. (24) holds, it means that the inclusion of the last hidden layer only produces a small relative performance improvement. In this case, the algorithm terminates and outputs $\mathcal{N}j$, which has $D_j = D{i−1}$ hidden layers. On the other hand, if Eq. (24) does not hold, including the last hidden layer to the network produces a noticeable improvement and the algorithm continues by building a new hidden layer at the next step.
根据Eq .(24)判断是否需要添加一个隐藏层,不添加就输出最终网络架构($\mathcal{N}_j$)
To enable a computationally tractable search space when optimizing a block of neurons, HeMLGOP adopts two architectural constraints.
The first constraint forces GOPs within the same block to share the same operator set assignment. Although this constraint might seem to promote homogeneity as in POP and its variants, it is not the case for networks constructed by HeMLGOP since each layer consists of multiple blocks, which can utilize different operator sets.
The second constraint is the fixed operator set assignment for the output layer. Similar to POPfast, the output layer in HeMLGOP only performs linear transformation, followed by a task-specific activation function, such as the softmax for classification tasks and the identity function for regression tasks. This constraint eliminates the need to optimize operator set assignment of the output layer in conjunction with the hidden layer as is done in POP.
HeMLGOP为了在优化一个block的神经元时启用易于处理的搜索空间,提出了两个架构约束
第一个架构约束是在同一个block中的GOPs使用相同的操作集,不同的block中的GOPs可以使用不同的操作集
第二个架构约束是与POPfast类似的对output layer对约束(松弛为线性转换并且跟着根据任务选择的适合的激活函数)
When HeMLGOP adds a new block of neurons to the current layer, all previous blocks are fixed (both the operator set assignments and synaptic weights), and the algorithm searches for the best performing operator set for the new block and optimizes its weights along with the weights of the output layer. To select a suitable operator set for the new block, the algorithm relies on randomization to evaluate the fitness of a given assignment. Specifically, for each operator set, HeMLGOP assigns the operator set to the new block and its parameters are randomly initialized from a uniform distribution. The parameters of the output layer are determined by solving the linear regression problem using the representation of the last hidden layer as input, that is,
where $\boldsymbol{H}$ denotes the outputs of the current hidden layer and $\boldsymbol{Y}$ denotes the targets. After the parameters of the output layer are computed, the performance is measured for this operator set assignment. After iterating through all operator sets, HeMLGOP selects the operator set leading to the best performance, and the parameters of the new block and the output layer are optimized using stochastic gradient descent for few epochs. This intermediate finetuning process is essential in order to fully take advantage of the modeling capacity of the new block of GOPs.
提出HeMLGOP添加一个新的神经元块时的操作:
- 固定之前的所有块的操作集和突触权重
- 为新的神经元块选择和分配适合的操作集和权重(根据均匀分布随机初始化,然后优化)
- 计算输出层的参数:根据最后一个隐藏层的表示作为输入来解决线性回归问题确定的,并给出如上公式。
- 计算完成输出层的参数后,评估该操作集的性能,再遍历所有操作集后选择最佳性能的操作集
- 确定最佳性能的操作集后,使用随机梯度下降优化新的神经元块和输出层的参数
Similar to POP and its variants, once the final network architecture has been determined, all parameters of the network can be jointly optimized using stochastic gradient descent with a small learning rate to further improving performance. Here, we should note that this final finetuning step is only beneficial when sufficient training data is available. On the other hand, when the training data is scarce, jointly finetuning all parameters can easily lead to overfitting.
类似于POP及其变体,一旦确定了最终的网络架构,就可以使用随机梯度下降和较小的学习率联合优化网络的所有参数,以进一步提高性能。
应该注意到,当有足够的训练数据可用时,这个最终的微调步骤才是有益的
另一方面,当训练数据稀缺时,联合微调所有参数很容易导致过度拟合。
Due to its computational efficiency and the ability to produce very compact network architectures, HeMLGOP has been applied to many applications such as face verification [37], learning to rank [38], and financial forecasting with imbalanced data [39]. The implementations of HeMLGOP and other related algorithms are publicly available as a standard Python package [40], which allows easy installation and further development.
给出HeMLGOP目前的实际应用场景
9.2.5 Subset sampling and online hyperparameter search for training enhancement
Up until now, we have covered different progressive neural network learning algorithms with different network construction and optimization strategies. A common characteristic in progressive neural network learning algorithms is that they require repetitive computations using the training data, regardless of the optimization approach adopted. This characteristic can lead to a large amount of computation and long training time, especially for those that rely on stochastic gradient-based optimization.
It was recently demonstrated in [41] that such repetitive computations over the training data can be reduced while achieving similar or better performance. Two key ideas were proposed in [41], which are the use of subsets of training data instead of the whole training set and the use of different hyperparameter values at different learning steps.
首先提出前面提到的progressive neural network learning algorithm的缺点:对训练数据重复计算
提出 使用子数据集 并且 不同的训练步骤使用不同的超参数 可以减少重复计算(性能相同或更好)
The advantage of using only a small subset of the training data optimizing the new connections at each incremental learning step is two-fold. In addition to the obvious computational cost reduction per incremental step, the use of different samples to train different groups of neurons also promotes neurons of different groups to capture different patterns in the data. In fact the idea of using a subset of available data to optimize a learning model is not new. In the field of active learning where the algorithms need to pick the most representative samples among a big pool of samples to be labeled, subset selection procedure plays a central role [42–44].
Different from active learning, the sample selection strategy for progressive learning can take advantage of the label information. The following three subset selection strategies were used in [41]:
- Random uniform selection: at each progressive learning step, select randomly $M$ samples from the training set of $N$ samples ($M \lt N$).
- Top-M selection based on training error: at each progression learning step, select the $M$ samples that induce the highest loss values, given the current network architecture.
- Top-M selection based on diverse training error: K-means clustering is applied to the predicted vectors and for each cluster, select $\lfloor M/C \rfloor$ samples with $C$ denoting the number of clusters and $\lfloor \cdot \rfloor$ is the floor operator.
提出仅使用小的训练集的子集进行优化的优势。并且提出在active learning中的使用
提出progressive learning的子集选择策略
- 随机均匀选择:每个步骤从$N$个样本中选择$M$个
- 基于训练误差的TOP-M选择:选择最终误差最高的$M$个样本
- 基于不同训练误差的TOP-M选择:根据K-means聚类为$C$个簇,选择$\lfloor M/C \rfloor$个样本
The key observation when using a subset of training data in [41] is that the number of unique samples that an algorithm uses during progressive learning is an important factor for the final performance.
For this reason, despite being unsupervised (without using the label information) and simple, random sampling achieves very good performance. The other two subset selection strategies can lead to a strong bias toward difficult samples, thus resulting in less diverse subsets of data being presented to the networks.
提出一个重要的观察结论:独特样本的数量是一个影响最终性能的重要因素
根据上述原因得出结论:第一种子集选择策略比其他两种更好
The second idea for enhancing performance of progressive network learning methods proposed by [41] is the incorporation of online hyperparameter search. In all algorithms described above the values of hyperparameters are fixed throughout the whole network construction phase. The best hyperparameter combination is often determined by running the method multiple times, measuring the performance of all runs on the validation set, and choosing the hyperparameter values leading to the best validation performance, which are then shared for the construction of all layers of the network. The process is both time-consuming and suboptimal. Since PNNL algorithms gradually increase the capacity of the neural network at each step, it is intuitive that the network might require different amount of regularization at different steps.
To search for a suitable hyperparameter setting, let $\mathcal{H}$ denote the set of all hyperparameter value combinations, and $Q$ be the cardinality of $\mathcal{H}$. At step $k$, after determining the subset $S_k$ of the training data, we solve $Q$ optimization problems using $S_k$ and $Q$ different configurations of hyperparameters. The algorithm then selects the solution that achieves the best performance on the validation set for the current step $k$.
提出为什么要在不同的训练阶段选择不同的超参数
提出设置合适超参数的方法:在的到第$k$层的训练数据子集$S_k$后,然后利用$S_k$和Q的不同配置的到最终的$\mathcal{H}$
9.3 Compressive learning
The classical signal processing pipeline often involves separate steps of signal acquisition, compression, storage, or transmission, followed by reconstruction and analysis.
In order to ensure high-fidelity reconstruction, an analog signal should be sampled at a rate that is twice the highest frequency component in the signal, the so-called Nyquist rate. However, for a certain class of signals possessing sparse or compressible representation in some domain, the Compressive Sensing (CS) theory guarantees that near perfect reconstruction is possible even when the signals are sampled at sub-Nyquist rates [45,46].
In fact, many signals that we encounter in the real-world often possess this property. For example, smooth signals are compressible in the Fourier domain or some piecewise smooth signals such as consecutive frames in a video have sparse coefficients in wavelet domain.
这里提出了一个pipeline的概念,pipeline相当于是一个流水线,即在这种任务中通常都需要依次执行的步骤。提出在经典的信号处理pipeline中通常涉及信号采集、压缩、存储、传输的步骤然后重建和分析。
为了确保高保真重建,应该以信号中最高频率分量的两倍的速率对模拟信号进行采样,即Nyquist rate。然而,对于某一域中具有稀疏或可压缩表示的某些信号,CS理论保证了即使信号以sub-Nyquist rates采样。
事实上,我们在现实世界中遇到的许多信号往往具有此属性。例如,平滑信号在傅里叶域中是可压缩的,或者视频中连续帧等一些分段平滑信号在小波域中具有稀疏系数。
Different from the classical signal acquisition approach, CS combines the signal sampling and compression steps at the sensor level. What we obtain from a CS device is a few compressed measurements of the signal, rather than the full amount of samples that has been obtained by sensing and discretization at a rate higher than the Nyquist rate. The compression step in CS is simply a linear projection of the samples to a lower dimension, making it highly efficient to be implemented on the sensor. Although this approach can provide a great solution for those scenarios where storing or transmitting the full signal is infeasible, working with the compressed measurements is often a daunting task. For example, a considerable amount of effort has been dedicated to develop signal recovery algorithms from compressed measurements, providing insights and theoretical conditions for a perfect reconstruction [45–47].
与传统的信号采集方法不同,CS在传感器级结合了信号采样和压缩步骤。我们从CS设备获得的是信号的一些压缩测量值,而不是通过以高于Nyquist rate的速率感测和离散化获得的全部样本量。CS中的压缩步骤只是将样本线性投影到较低的维度,从而使其在传感器上高效实现。尽管这种方法可以为那些存储或传输完整信号不可行的场景提供一个很好的解决方案,但使用压缩的测量往往是一项艰巨的任务。例如,大量的工作致力于从压缩测量中开发信号恢复算法,为完美重建提供见解和理论条件。
前面都是在介绍CS,为CL作铺垫
Although signal recovery is necessary and important in some applications such as the reconstruction of Magnetic Resonance Imaging (MRI) images for visual diagnosis by medical experts, there are many applications that do not explicitly require signal recovery. For example, object detection is often the primary task in many radar applications. Furthermore, signal reconstruction can be undesirable in sensitive scenarios since this step can potentially reveal private information, leading to the infringement of data protection legislation. Because of these reasons, it is natural to consider the problem of learning from compressed measurements without reconstruction, which is referred to as Compressive Learning (CL) in literature. While CS has been extensively studied and covered, literature on CL is rather scattered despite its high potential for robotic and IoT applications.
In the following, we will cover CL methodologies, which can be categorized into two groups, namely vector-based CL and tensor-based CL. The main difference between the two categories lies in the way the compressed measurements are obtained. For vector-based CL methods, the signal acquisition model contains a single CS operator, considering the input signal as a vector while in tensor-based CL methods, the signal acquisition model adopts multiple separable CS operators, considering the input as a multidimensional signal.
提出压缩学习的概念:在没有重构的情况下从压缩测量中学习
介绍vector-based CL和tensor-based CL,并介绍两者的不同
- vector-based CL:基于一个CS operator
- tensor-based CL:基于多个CS operator
In the following, we denote scalar values by either lowercase or uppercase letters $(x, y, X, Y, \dots)$, vectors by lowercase boldsymbolface letters $(\boldsymbol{x}, \boldsymbol{y}, \dots)$, matrices (2D tensor) by uppercase boldsymbolface letters $(\boldsymbol{X}, \boldsymbol{Y}, \Phi , \dots)$, and tensor as calligraphic capital letters $(\mathcal{X} , \mathcal{Y}, \dots)$.
规定scalar values、vectors、matrices、tensor在后文的符号定义
9.3.1 Vector-based compressive learning
One of the main components of vector-based CL (hereafter we simply refer to as CL) methods is the CS component, which takes as input a signal representing by vector $\boldsymbol{y} \in \mathbb{R}^I$. As we mentioned before, the signal of interest in CS is assumed to have a sparse or compressible representation $\boldsymbol{x} \in \mathbb{R}^J$ in some basis (or dictionary) $\Psi \in \mathbb{R}^{I \times J}$ . That is, $\boldsymbol{y}$ can be expressed as a linear combination of atoms (columns) of the dictionary $\Psi$, with $\boldsymbol{x}$ being the combination coefficients:
where $\Vert x \Vert_0$ denotes the number of non-zero elements in $\boldsymbol{x}$, which reflects the degree of sparsity in the signal. When $J > I$ , which is the case frequently adopted in CS literature, $\Psi$ is called an overcomplete dictionary.
Vector-based CL的核心组件是CS组件,并且规定$\boldsymbol{y}$作为CS组件的输入,并且$\boldsymbol{x}$为压缩表示根据$\Psi$的压缩表示,即$\boldsymbol{y} = \Psi\boldsymbol{x}$,$\Psi$可以看成一个字典,表示那些列的值不为0
In CS, the signal $\boldsymbol{y}$ is compressed by a linear projection to a lower-dimensional space:
where $\boldsymbol{z} \in \mathbb{R}^M, M \lt I$ denotes the compressed measurements, which correspond to the output of a CS device. $\Phi \in \mathbb{R}^{M \times I}$ denotes the sensing operator, which is the matrix representing the linear projection performed by the CS device.
给出CS的输出映射公式,通过$\Phi$与输入$\boldsymbol{y}$相乘,其中$\Phi$为线性投影矩阵
In literature, Eqs. (26) and (27) are often combined into a single equation, which is referred to as the CS model:
将上述两个公式结合
The main problem considered in CS is the recovery of $\boldsymbol{y}$ from the compressed measurement $\boldsymbol{z}$.
As such, a standard approach when building a learning model with data obtained from a CS device is to simply apply methods that have been developed for uncompressed signal and learn a decision function $f (\tilde{y})$, where $\tilde{y}$ denotes the reconstructed signal.
While being straightforward, this approach includes the signal reconstruction step, which is computational expensive.
提出CS的主要问题:根据$\boldsymbol{z}$恢复为$\boldsymbol{y}$
提出一种标准方法:在利用从 CS 设备获取的数据建立学习模型时,标准方法是简单地应用针对未压缩信号开发的方法,并学习决策函数 $f(\tilde{y})$,其中 $\tilde{y}$ 表示重建信号
提出这种方法很浪费计算资源
The idea of learning a decision function based on the compressed measurements, that is, $f(\boldsymbol{z})$, was introduced by [48].
In this work, the problem of learning in the compressed domain from the maximum likelihood perspective was investigated. Using the maximum likelihood principle, it was suggested that a given classification accuracy is only dependent on the noise level, which is independent of the underlying sparsity of the images.
In addition, the generalized maximum likelihood framework was employed to investigate the effects of geometric transformations with respect to the classification performance, and it was found out that the number of measurements required grows linearly with the dimensionality of the manifold formed by the set of transformed images, such that a certain accuracy level of the generalized maximum likelihood classifier is maintained.
Finally, the matched filter classifier (a special case of the generalized maximum likelihood classifier) was applied in the compressed domain, leading to the so-called smashed filter algorithm. The smashed filter algorithm was further extended to the classification of human actions [49], where 3D correlation filters along the spatial and temporal dimension were applied to extract features from compressed measurements of video frames. In addition to action recognition, the smashed filter concept was also applied to compressively sensed facial images for face recognition [50].
提出基于压缩测量的决策函数$f(\boldsymbol{z})$
研究发现,给定的分类准确性仅依赖于噪声水平,而与图像的潜在稀疏性无关
此外,还利用广义最大似然框架研究了几何变换对分类性能的影响,发现所需测量的数量与由变换图像集形成的流形的维度线性增长,以保持广义最大似然分类器的准确性水平
最后,将匹配滤波器分类器(广义最大似然分类器的特例)应用于压缩域,得到了smashed filter算法。该算法进一步扩展到人类动作分类,其中应用了3D相关滤波器沿空间和时间维度从视频帧的压缩测量中提取特征。除了动作识别外,smashed filter概念还被应用于压缩感知的面部图像进行人脸识别。
In several works in CS, a random sensing operator is often considered. Given a random sensing operator, theoretical work on random linear projections of smooth manifolds provides an important result for learning a linear classifier on the compressed domain [51]. This analysis suggests that a small number of random linear projections can faithfully preserve geometric information of a signal lying on a smooth manifold. More specifically, it was shown that there exists a sufficient number of projections $M$ such that, with high probability, the pairwise Euclidean and geodesic distances between points on the manifold are preserved under the given random projections. This result implies that the performance of a linear classifier in the compressed domain can match the performance of the same classifier in the original signal domain.
少量的随机线性投影可以保留位于光滑流形上的信号几何信息
结果表明:线性分类器在压缩域中的性能可以与相同分类器在原始信号域中的表现相匹配
While the aforementioned theoretical work was only developed in the general context of random projections of smooth manifolds, without any empirical results demonstrated in CL, the work in [52] (which was also the first to introduce the term compressive learning) provided a similar theoretical result for the Support Vector Machine (SVM) classifier with empirical verification, focusing on the problem of learning from compressed measurements. Specifically, the analytical bounds for training a linear SVM using compressed measurements $\boldsymbol{z}$ were derived, indicating that when the sensing matrix satisfies the distance-preserving property, the performance of a linear SVM operating on $\boldsymbol{z}$ is equivalent to the performance of a best linear threshold classifier operating on the original signal $\boldsymbol{y}$. This theoretical result was also supported by experiments in image texture classification.
前面提出的结论是经验性结论,这段内容根据提出了实验性结论
The work in [53] focusing on the class of signals that are described by the Gaussian Mixture Model (GMM) also contributed to theoretical analysis of CL. In this work, the source signal is assumed to follow the GMM model, which is motivated from the fact that natural image patches can be successfully modeled by GMMs. The GMM that describes the source signal is also assumed to be known in the analysis. An upper bound to the probability of misclassification of the maximum-a-posteriori classifier was derived, given that the sensing matrix is drawn from a zero-mean Gaus-sian distribution and the compressed measurements were contaminated with standard white Gaussian noise.
总结了文献[53]中关于压缩学习(CL)的理论分析工作,特别是针对高斯混合模型(GMM)描述的信号类。在这个工作中,假设源信号遵循GMM模型,这是基于自然图像块可以成功用GMMs建模的事实。在分析中还假设描述源信号的GMM是已知的。推导出了最大后验分类器误分类概率的上界,条件是感知矩阵来自零均值高斯分布,且压缩测量受到标准白高斯噪声的污染。
While early works in CL focus on providing theoretical insights of simple models operating on compressed domains, such as linear models, later works shifted toward the practicality of CL for real-world problems by utilizing nonlinear learning models and focusing more on empirical validation. Since the emergence in the ImageNet Large Scale Visual Recognition Challenge 2012, deep neural networks have become a de facto choice for learning nonlinear relationships. They soon made their entrance into the CL literature in [54], where a Convolutional Neural Network (CNN) was used to classify compressed measurements of handwritten character images obtained from a random sensing matrix. The empirical results in [54] showed that a nonlinear classifier such as CNN can yield superior performance compared to smashed filters. Furthermore, the experimental results in this work also suggested that the CL paradigm can produce relatively good classification performance even when the compression rate is up to $100\times$.
根据文献[54]中的结果,像CNN这样的非线性分类器可以产生比上述smashed filters有更高的性能即使压缩率高达100倍,CL范式也能产生较好的分类性能
The idea of combining CS and deep learning was further refined by the works in [55,56], where the idea of end-to-end CL learning was first introduced. That is, instead of utilizing a random sensing operator as predominantly done in prior works, the algorithm jointly optimizes both the machine learning model and the sensing operator via stochastic gradient descent. Since the linear projections in CS are optimized in conjunction with the classifier toward minimizing the learning objective, they are better at capturing the relevant information for the learning problem from the source signal. As a result, the approach proposed in [55,56] achieved far better performance when compared to the case where random sensing matrices were applied. In addition, later works have soon adopted and extended this idea to different applications [57–59].
文献[55,56]结合CS和深度学习的思想,介绍了端到端CL学习的思想,通过随机梯度下降对机器学习模型和感知算子进行联合优化。
The end-to-end CL architecture for RGB image recognition proposed by [56] is illustrated in Fig. 9.7. As we can see from this figure, after obtaining the compressed measurements $\boldsymbol{z}_R , \boldsymbol{z}_G , \boldsymbol{z}_B$ from the R, G, B color channels respectively, a reprojection step is applied to the compressed measurements by linearly up-sampling them using the transpose of the corresponding sensing operator, that is, $\boldsymbol{t}_R = \Phi^T_R \boldsymbol{z}_R , \boldsymbol{t}_G = \Phi^T_G\boldsymbol{z}_G ,\boldsymbol{t}_B = \Phi^T_B \boldsymbol{z}_B$ . After performing an appropriate reshaping step, the up-sampled fea-tures are introduced to a CNN. As parameter initialization is an important step in stochastic optimization, the sensing matrices R , G , B are initialized such that the mean squared reconstruction error is minimized. The CNN classifier is initialized with weights learned from uncompressed data. After the initialization step, all parameters are updated with stochastic gradient descent.
解释在文献[56]中提出的的方法
9.3.2 Tensor-based compressive learning
先给出一些关于tensor的符号表示和计算公式
再介绍MCL
然后介绍MCLwP(MCL的一种变体)
While the majority of signals that we encounter appear naturally in tensor form, the CL paradigm described in the previous section only considers a sensing model for signals represented as vectors. The multidimensional representation of a signal often exhibits natural semantic differences inherent in different dimensions of the signal. For this reason, it is desirable to design learning models that are capable of exploiting the tensor structure of the data.
Regarding the problem of learning from compressed measurements, Multilinear Compressive Learning (MCL) which is a CL framework that takes into account the multidimensional structure of signals naturally represented in the tensor form was proposed in [60].
大多数信号都是以张量形式自然出现的
[60]中提出了多线性压缩学习(MCL),它是一种考虑了以张量形式自然表示的信号的多维结构的CL框架
Before diving into the details of MCL, it is necessary to review some important notions and properties in multilinear algebra. The term mode is often used to refer to the dimension of a tensor. For example, a tensor $\mathcal{X} \in \mathbb{R}^{I1 \times \cdots \times I_k \times \cdots \times I_K}$ is said to have $K$ modes with the dimension of the $k$th mode being equal to $I_k$ . One of most important operations in multilinear algebra is the mode-$k$ product, which defines the product between a tensor and a matrix. The mode-k product between a tensor $\mathcal{X} = [x{i1} , \dots , x{i_K} ] \in \mathbb{R}^{I_1 \times \dots I_k \times \dots \times I_K}$ and a matrix $\boldsymbol{W} \in \mathbb{R}^{J_k \times I_k}$ is another tensor of size $I_1 \times \cdots \times J_k \times \cdots \times I_K$ and denoted by $\mathcal{X} \times _k \boldsymbol{W}$. The elements of $\mathcal{X} \times _k\boldsymbol{W}$ are defined as
回顾和定义符号表示,重点定义了tensor的表示和$\mathcal{X} \times _k\boldsymbol{W}$,参考:tensor的mode-n展开和mode-n乘积理解
简单来说:
对于三维tensor$\mathcal{X}(I_1, I_2, I_3)$
- 第一个mode(mode-1):$\mathcal{X}(:,I_2, I_3)$;
- 第二个mode(mode-2):$\mathcal{X}(I_1,:,I_3)$;
- 第三个mode(mode-3):$\mathcal{X}(I_1,I_2,:)$
When multiplying a tensor with multiple matrices along different modes, we often chain together the notation, that is,
denotes the multiplication of tensor $\mathcal{X}$ with $\boldsymbol{W}_1$ along the first mode, with $\boldsymbol{W}_2$ along the second mode and so on.
For a series of multiplications in distinct modes, the order of computation does not affect the result. That is,
给出tensor与不同mode的矩阵相乘时的链式表达,并且结果与乘法的顺序无关(可交换)
In addition to mode-$k$ product, another operation that involves two matrices exists, which is the Kronecker product. The Kronecker product between two matrices $\boldsymbol{A} \in \mathbb{R}^{M \times N}$ and $\boldsymbol{B} \in \mathbb{R}^{P \times Q}$ is denoted as $\boldsymbol{A} \otimes \boldsymbol{B}$. The result is a matrix which has $MP \times NQ$ elements and is calculated by
除了mode-$k$ product,又给出Kronecker product的表示。更详细内容参考克罗内克积
Using the Kronecker product definition, we can express a series of mode-$k$ products by a vector-matrix multiplication. This means that
can be implemented as follows:
where $\boldsymbol{y} = \text{vec}(\mathcal{Y})$ and $\boldsymbol{x} = \text{vec}(\mathcal{X})$, with $\text{vec}(\cdot)$ denoting the vectorization operation.
利用Kronecker Product表达多个mode的矩阵相乘的链式表达,其中$\boldsymbol{x}$和$\boldsymbol{y}$时tensor的向量化表示(就是把tensor中的每个元素排列在一个向量中)
例如:
2*2的二维tensor:$[a{11}, a{12}, a{21},a{22}]$.
3*3*3的三维tensor:$[a{111}, a{211},a{311}, a{121}, a{221}, a{321}, a{131}, \dots,a{233}, a_{333}]$
In order to retain the multidimensional structure of the source signal, it is necessary to acquire and compress the source signal so that the structural information is captured in the compressed measurements. MCL uses the Multilinear Compressive Sensing (MCS) model for this purpose. Let us denote a source signal having multidimensional structure as $\mathcal{Y} \in \mathbb{R}^{I_1\times\cdots \times I_K}$ . Instead of using the assumption that $\text{vec}(\mathcal{Y})$ is sparse with respect to some dictionary as in CS, the MCS model assumes that $\mathcal{Y}$ is sparse with respect to a set of dictionaries $(\Psi_1, \cdots , \Psi_K )$, and $\mathcal{Y}$ can be represented by a sparse Tucker model [61]:
给出源信号$\mathcal{Y}$的稀疏Tucker model表示
The source signal $\mathcal{Y}$ can be acquired in a compressed manner while retaining its tensor structure by using a set of linear sensing operators along each mode:
where $\Phi_k \in \mathbb{R}^{M_k \times I_k}, (M_k \lt I_k)$ denotes the sensing operator in the $k$th mode and $\mathcal{Z} \in \mathbb{R}^{M_1\times\cdots\times M_K}$ denotes the compressed measurement obtained from the sensor.
给出根据源信号$\mathcal{Y}$经过线性传感器操作得到压缩测量值的公式
Here, we should note that the MCS model can be easily implemented using the standard CS hardware by using the property mentioned in Eqs. (33) and (34). That is, the set of separable sensing operators $(\Phi_1, \dots , \Phi_K )$ in MCS can be combined into a single sensing operator $(\Phi \in \mathbb{R}^{(M_1\dots M_K )\times(I_1\dots I_K))}$ using the Kronecker product $(\Phi = \Phi_1 \otimes \cdots \otimes \Phi_K )$, and $\mathcal{Z}$ is obtained, after appropriate reshaping, via
将上一个公式的$\Phi_1\dots,\Phi_K$聚合为$\Phi = \Phi_1 \otimes \cdots \otimes \Phi_K$,并给出向量化表示
Beside the fact that multidimensional structures of the source signal are preserved in the MCS model, this sensing model significantly reduces the memory and computational complexity of the sensing step. In order to observe this, let us take as an example the task of sensing and compressing grayscale images of size $1080 \times 1920$ with a compression rate of $100\times$. Using the CS model in Eq. (27), we need to store a sensing matrix of size $(1080 ∗ 1920) × (108 ∗ 192)$, having approximately 42.9 billion parameters, while with the same compression rate, we only need to store two sensing matrices of size $1080 × 108$ and $1920 × 192$, having approximately 0.5 million parameters.
sensing model可以明显降低内存和计算复杂度,并给出一个计算例子
There are two other components in MCL, which are illustrated in Fig. 9.8, the Feature Synthesis (FS) component and the task-specific neural network ($\mathfrak{N}$). After obtaining the compressed measurement $\mathcal{Z}$ from a CS device, the MCL model synthesizes features $\mathcal$ from $\mathcal{Z}$ through the FS component, which contains multilinear operations that preserve the tensor structure in $\mathcal{Z}$:
where $\Theta_k \in \mathbb{R}^{P_k \times M_k}, (k=1,\dots, K)$ denotes the parameters of the FS component.
给出MCL的流程图,前面只介绍了compressed measurement($\mathcal{Z}$)的计算,这里给出通过$\mathcal{Z}$计算feature synthesis($\mathcal{T}$)的表达式
Here, we should note that the dimensions $(P_1 × · · · × P_K )$ of the synthesized feature T depend on the given learning task and the input specification of the taskspecific neural network. This is because the synthesized feature $\mathcal{T}$ is introduced to the third component of the MCL model, which is the task-specific neural network $\mathfrak{N}$, to generate predictions.
$\mathfrak{N}$ is a neural network that is often used to solve the same learning problem using uncompressed data. Thus the architecture of $\mathfrak{N}$ is selected depending on the learning task. For example, when the task is to detect objects from an image, $\mathfrak{N}$ can be a YOLO object detector [3].
应该注意feature synthesis的维数,因为它回作为task-specific network的输入
介绍task-specific network($\mathfrak{N}$)
The three components of the MCL model are optimized in an end-to-end manner using stochastic gradient descent. For the initialization of their parameters, the following strategy was proposed in [60].
Parameters of the task-specific neural network are initialized by training it with the set of uncompressed data:
where $\Theta\mathfrak{N}$ and $f{\mathfrak{N}}$ denote the parameters and the function representing $\mathfrak{N}$, respectively, $L(·)$ denotes the learning objective function, and $\tilde{\mathcal{Y}}_i$ and $c_i$ denote the available uncompressed data sample and the corresponding label.
Here, we should note that the uncompressed data ($\tilde{\mathcal{Y}}$) can be different from the source signal ($\mathcal{Y}$) that we wish to capture with the CS device. For example, to learn an MCL model for object detection, we might want to use available data sets with annotations such as the PASCAL data set or MS COCO data set at resolution $480 × 480 × 3$, while our CS device resolution is at $1080 × 1920$. In this case, the dimensions of $\tilde{\mathcal{Y}}$ are $480 × 480 × 3$ while the source signal $\mathcal{Y}$ has dimensions of $1080 × 1920$.
上述三个组件都使用梯度下降法用端到端的方式进行优化
task-specific neural network通过未被压缩的数据集的训练初始化
注意这里的$\tilde{\mathcal{Y}}$是未被压缩的数据集,但是它和源信号$\mathcal{Y}$也不同,举例给出长宽不同
Parameters of the sensing and FS component are initialized with values that minimize the following reconstruction error:
where $fS$ and $f{FS}$ denote the functions representing the sensing and FS component, respectively, and $‖ · ‖_F$ denotes the Frobenius norm.
Here, we should note that when we do not have access to the source signal $\mathcal{Y}i$ that corresponds to the uncompressed data $\tilde{\mathcal{Y}}_i$, we can imitate $\mathcal{Y}_i$ by applying an upsampling or downsampling method to $\tilde{\mathcal{Y}}_i$ to generate $\mathcal{Y}_i$ with the desired resolution.
给出传感器参数和FS组件的训练过程(通过实现上述公式)
可以使用上采样或下采样用$\tilde{\mathcal{y}}_i$产生具有对应分辨率的$\mathcal{Y}$
Experimental results in object classification and face recognition problems in [60] showed that by considering the multidimensional structure of images, the MCL model cannot only produce better classification performance but is also more efficient in terms of memory and computational cost, compared to the end-to-end CL framework proposed in [56] that considers the source signals in the form of vectors.
根据文献[60]中的实验结果,可以得出性能确实变好了
While the FS component proposed in [60] only consists of multilinear operations, the operations that extract features from the compressed measurements in general do not need to be linear or multilinear, as long as they are capable of preserving the multidimensional structure in $\mathcal{Z}$.
To take advantage of the modeling capability of nonlinear transformations, an extension of the MCL model that synthesizes nonlinear features from the compressed measurements was proposed in [62]. This extended MCL model is dubbed as multilinear compressive learning with prior knowledge (MCLwP) since it comes with a novel training method that can incorporate prior knowledge of a high-quality compressed domain and feature space into the target MCL model.
FS组件不需要时线性或多线性的,只要它们能够保留$\mathcal{Z}$中的多维结果即可
提出文献[62]中对MCL的扩展,该模型从压缩的测量中合成非线性特征。这种扩展的MCL模型被称为具有先验知识的多线性压缩学习(MCLwP),因为它提供了一种新的训练方法,可以将高质量压缩域和特征空间的先验知识合并到目标MCL模型中
In MCLwP a high-quality compressed domain for $\mathcal{Z}$ and feature space for $\mathcal{T}$ are discovered by training a prior model. This prior model also comprises of three components that correspond to the three components of an MCL model, that is, a nonlinear sensing component ($gS$), a nonlinear FS component ($g{FS}$), and a task-specific neural network ($g_\mathfrak{N}$).
The nonlinear sensing component of the prior model has several convolution layers with nonlinear activation and max-pooling layers to reduce dimensions of the source signal to target dimensions of the compressed measurements $\mathcal{Z}$.
On the other hand, the nonlinear FS component consists of several convolution layers with nonlinear activation and upsampling layers to transform $\mathcal{Z}$ to $\mathcal{T}$ .
The structure of the task-specific neural network is dependent on the learning task, thus similar to the MCL model. The prior model is optimized in the same manner as the MCL model. That is, before the end-to-end optimization step, the sensing and synthesis components are initialized with values that minimize the reconstruction error of the uncompressed data while the task-specific neural network is initialized by training on the uncompressed data.
介绍MCLwP,仍然具有与MCL对应的组件:非线性传感器$gS$、非线性FS组件$g{FS}$和task-specific network$g_\mathfrak{N}$
介绍非线性传感器组件的组成(多个卷积层,其中非线性激活层和最大池化层将源信号的维数降为压缩测量值$\mathcal{Z}$的目标维数)
介绍非线性FS组件
介绍task-specific network
After the prior model is optimized, its knowledge about the learning task from the compressed measurements is transferred to the target MCL model. Here, we should note that since there is no structural constraint on the FS component in a MCL model, it was proposed in [62] to use the same nonlinear structure that is used in the prior model for the FS component in the target MCL model.
The new optimization procedure for the target MCL using the prior model consists of three steps, which are illustrated in Fig. 9.9. In the first step, the MCS component is optimized to mimic the output of the nonlinear sensing component as follows:
In the second step, both the sensing and the FS components in the target MCL model are optimized to mimic the features synthesized by the prior model as follows:
In the last step, all components of the target MCL model are optimized to mimic the predictions generated by the prior model, as well as to minimize the learning objective using the labeled data as follows:
where $c_i, c_i^{(g)},$ and $c_i^{(f)}$ denote the true label, the prediction produced by the prior model and the target MCL model, respectively, $L_D()$ denotes a distillation loss, such as the proposed in [63], and $L(\cdot)$ denotes the learning objective function.
提出MCLwP的FS组件也使用与MCL相同的非线性结构
并给出MCLwP的三个组件的优化公式和结构图
While a highly nonlinear prior model is capable of discovering high-quality compressed domain and feature space, it is only effective when sufficient labeled data is available. When labeled data is scarce, a prior model can easily fall into the overfitting regime, exhibiting poor generalization. As a consequence, the resulting MCL model trained with bad prior knowledge will not generalize to unseen data. While labeled data can be expensive to obtain, in many cases, we can easily obtain data coming from the same distribution without any label.
In this scenario, the work in [62] also includes a semisupervised extension of the aforementioned training technique with a prior model. The key idea of this semi-supervised training method is on how the prior model can be trained to provide suggestive annotations for the unlabeled data, which is then used together with the labeled data to perform knowledge transfer.
A straightforward way to generate suggestive labels for the unlabeled data is to simply use the prior model that has been trained with a limited number of labeled samples to make predictions on the unlabeled samples. This approach, however, is defective since the prior model trained with a small number of samples without any further modification is likely to be overfitting, thus generating many false labels. To overcome this issue, [62] proposed a self-labeling process that incrementally updates the prior model and generates suggestive labels using a small number of unlabeled data at a time.
提出MCLwP是基于先验知识的,当标签数据缺乏时会很容易过拟和,并且标签数据不易获取(提出缺点)
文献[62]提出了一种半监督的扩展方法,并给出关键思想(给未标记的数据生成暗示性的标签)
提出实现半监督的一种方法(直接使用先验模型训练未标记的数据),但是先验模型还是过拟和的,因此不合适。文献[62]又提出一种自标记过程,该过程增量地更新先前的模型,并每次使用少量未标记的数据生成暗示性标签。
Let us denote the set of labeled data as $\mathfrak{L} = {(\mathcal{Y}_i , \tilde{\mathcal{Y}}, c_i )|i = 1, . . . , N }$ and the set of unlabeled data as $\mathfrak{U} = {(\mathcal{Y}_j , \tilde{\mathcal{Y}}_j )|j = N + 1, . . . , M}$.
At first, the nonlinear sensing and FS components of the prior model are initialized with values that minimize the reconstruction error of the uncompressed data. Since the label information is not required in this step, both labeled and unlabeled data can be used. Similar to the supervised version, the task-specific network is initialized with uncompressed data from the labeled set.
After initialization, all components of the prior model are trained in an end-to-end manner to optimize the learning objective using the incrementally enlarged label set $\tilde{\mathfrak{L}}$. Initially, the enlarged label set only contains samples from the labeled set, that is, $\tilde{\mathfrak{L}} = \mathfrak{L}$. After every $T$ back-propagation epochs, $\tilde{\mathfrak{L}}$ is expanded with those samples (and their predicted labels) in $\mathfrak{U}$ that have the most confident predictions from the current prior model, given a probability threshold $ρ$. That is,$\tilde{\mathfrak{L}} = \tilde{\mathfrak{L}} ∪ \mathfrak{C}$, with $\mathfrak{C}$ defined as
After each iteration of this process, the samples added to $\tilde{\mathfrak{L}}$ are removed from the unlabeled set, that is, $\mathfrak{U} = \mathfrak{U} \setminus \mathfrak{C}$. The optimization procedure terminates when $\mathfrak{C} = \varnothing$.
给出标记数据和未标记数据的符号表示
同时使用标记和未标记数据对nonlinear sensing和 FS components进行初始化
开始训练时只使用标记数据,再经过$T$个epoch后添加最可靠预测的未标记样本(超过概率阈值$\rho$的样本),这部分未标记样本表示在集合$\mathfrak{C}$中,并给出$\mathfrak{C}$的定义。
给出优化过程的终止条件
The final set $\tilde{\mathfrak{L}}$ and the prior model are used to train the target MCL model in a similar manner as in the supervised algorithm. That is, the optimization steps are the same as in Eqs. (41), (42), and (45), except that the sum is computed over the samples in $\tilde{\mathfrak{L}}$. It has been shown in [62] that using a prior model, an MCL model can obtain noticeable performance gains. In addition, the semisupervised training method described above can indeed alleviate the overfitting problem when only few samples have labels.
使用最终训练得到的数据集$\tilde{\mathfrak{L}}$和prior model进行训练。根据实验结果表明,上述方法确实可以缓解过拟和问题
While the computational advantage of the MCL over vector-based CL is obvious, it is unclear how the dimensions of the compressed measurement $\mathcal{Z}$ should be selected, given a target compression rate. For example, when the dimensions of the source signal are $100×100$ and the compression rate is 100×, there are multiple ways to specify the dimensions of $\mathcal{Z}$, such as $10 × 10$ or $20 × 5$ or $25 × 4$ and so on. It would require a large number of experiments to determine the best configuration for $\mathcal{Z}$. In addition to $\mathcal{Z}$, in a real-world problem there is also the need to determine optimal values for the CS device resolution ($\mathcal{Y}$) as well as the dimensions of uncompressed data ($\tilde{\mathcal{Y}}$). The work in [64] addressed this problem through an empirical study and suggested a performance indicator that can help us determine such information without conducting the entire optimization process of the MCL model. Specifically, it was found that the mean-squared errors obtained during the initialization of the sensing and FS components in Eq. (40) highly correlates with the final classification errors. This finding suggests that in order to produce an estimate ranking between different dimension configurations, conducting only the initialization steps in the MCL model is sufficient, thus the overall computational cost of training multiple MCL models for model selection can be highly reduced.
了在不同维度配置之间产生估计排序,只需在MCL模型中进行初始化步骤就足够了,从而可以大大降低训练多个MCL模型进行模型选择的总体计算成本。
References
[1] S. Ren, K. He, R. Girshick, J. Sun, Faster r-cnn: towards real-time object detection with region proposal networks, IEEE Transactions on Pattern Analysis and Machine Intelligence 39 (6) (2016) 1137–1149.
[2] K. He, G. Gkioxari, P. Dollár, R. Girshick, Mask r-cnn, in: Proceedings of the IEEE International Conference on Computer Vision, 2017, pp. 2961–2969.
[3] J. Redmon, A. Farhadi, Yolov3: an incremental improvement, arXiv preprint, arXiv:1804. 02767, 2018.
[4] Z. Cao, G. Hidalgo, T. Simon, S.-E. Wei, Y. Sheikh, Openpose: realtime multi-person 2d pose estimation using part affinity fields, IEEE Transactions on Pattern Analysis and Machine Intelligence 43 (1) (2019) 172–186.
[5] A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A.N. Gomez, Ł. Kaiser, I. Polosukhin, Attention is all you need, Advances in Neural Information Processing Systems 30 (2017) 5998–6008.
[6] J. Devlin, M.-W. Chang, K. Lee, K. Toutanova Bert, Pre-training of deep bidirectional transformers for language understanding, arXiv preprint, arXiv:1810.04805, 2018.
[7] Z. Dai, Z. Yang, Y. Yang, J. Carbonell, Q.V. Le, R. Salakhutdinov, Transformer-xl: attentive language models beyond a fixed-length context, arXiv preprint, arXiv:1901.02860, 2019.
[8] D.T. Tran, A. Iosifidis, J. Kanniainen, M. Gabbouj, Temporal attention-augmented bilinear network for financial time-series data analysis, IEEE Transactions on Neural Networks and Learning Systems 30 (5) (2018) 1407–1418.
[9] Z. Zhang, S. Zohren, S. Roberts, Deeplob: deep convolutional neural networks for limit order books, IEEE Transactions on Signal Processing 67 (11) (2019) 3001–3012.
[10] K. He, X. Zhang, S. Ren, J. Sun, Deep residual learning for image recognition, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016, pp. 770–778.
[11] G. Huang, Z. Liu, L. Van Der Maaten, K.Q. Weinberger, Densely connected convolutional networks, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017, pp. 4700–4708.
[12] A. Krizhevsky, I. Sutskever, G.E. Hinton, Imagenet classification with deep convolutional neural networks, Communications of the ACM 60 (6) (2017) 84–90.
[13] T. Elsken, J.H. Metzen, F. Hutter, Neural architecture search: a survey, arXiv preprint, arXiv:1808.05377, 2018.
[14] D. Blalock, J.J.G. Ortiz, J. Frankle, J. Guttag, What is the state of neural network pruning?, arXiv preprint, arXiv:2003.03033, 2020.
[15] I. Hubara, M. Courbariaux, D. Soudry, R. El-Yaniv, Y. Bengio, Quantized neural networks: training neural networks with low precision weights and activations, Journal of Machine Learning Research 18 (1) (2017) 6869–6898.
[16] Y. Choukroun, E. Kravchik, F. Yang, P. Kisilev, Low-bit quantization of neural networks for efficient inference, in: 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), IEEE, 2019, pp. 3009–3018.
[17] M. Jaderberg, A. Vedaldi, A. Zisserman, Speeding up convolutional neural networks with low rank expansions, arXiv preprint, arXiv:1405.3866, 2014.
[18] D.T. Tran, A. Iosifidis, M. Gabbouj, Improving efficiency in convolutional neural networks with multilinear filters, Neural Networks 105 (2018) 328–339.
[19] X. Yu, T. Liu, X. Wang, D. Tao, On compressing deep models by low rank and sparse decomposition, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017, pp. 7370–7379.
[20] Y. Cheng, D. Wang, P. Zhou, T. Zhang, A survey of model compression and acceleration for deep neural networks, arXiv preprint, arXiv:1710.09282, 2017.
[21] B. Wu, X. Dai, P. Zhang, Y. Wang, F. Sun, Y. Wu, Y. Tian, P. Vajda, Y. Jia, K. Keutzer, Fbnet: hardware-aware efficient convnet design via differentiable neural architecture search, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2019, pp. 10734–10742.
[22] F. Scheidegger, L. Benini, C. Bekas, A.C.I. Malossi, Constrained deep neural network architecture search for iot devices accounting for hardware calibration, in: Advances in Neural Information Processing Systems, 2019, pp. 6056–6066.
[23] C.P. Chen, Z. Liu, Broad learning system: an effective and efficient incremental learning system without the need for deep architecture, IEEE Transactions on Neural Networks and Learning Systems 29 (1) (2017) 10–24.
[24] S. Kiranyaz, T. Ince, A. Iosifidis, M. Gabbouj, Progressive operational perceptrons, Neurocomputing 224 (2017) 142–154.
[25] S. Chatterjee, A.M. Javid, M. Sadeghi, P.P. Mitra, M. Skoglund, Progressive learning for systematic design of large neural networks, arXiv preprint, arXiv:1710.08177, 2017.
[26] D.T. Tran, S. Kiranyaz, M. Gabbouj, A. Iosifidis, Heterogeneous multilayer generalized operational perceptron, IEEE Transactions on Neural Networks and Learning Systems 31 (3) (2019) 710–724.
[27] D.T. Tran, S. Kiranyaz, M. Gabbouj, A. Iosifidis, Progressive operational perceptrons with memory, Neurocomputing 379 (2020) 172–181.
[28] Y.-H. Pao, Y. Takefuji, Functional-link net computing: theory, system architecture, and functionalities, Computer 25 (5) (1992) 76–79.
[29] Y.-H. Pao, G.-H. Park, D.J. Sobajic, Learning and generalization characteristics of the random vector functional-link net, Neurocomputing 6 (2) (1994) 163–180.
[30] S. Feng, C.P. Chen, Fuzzy broad learning system: a novel neuro-fuzzy model for regression and classification, IEEE Transactions on Cybernetics 50 (2) (2018) 414–424.
[31] M. Han, S. Feng, C.P. Chen, M. Xu, T. Qiu, Structured manifold broad learning system: a manifold perspective for large-scale chaotic time series analysis and prediction, IEEE Transactions on Knowledge and Data Engineering 31 (9) (2018) 1809–1821.
[32] S. Boyd, N. Parikh, E. Chu, Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers, Now Publishers Inc., 2011.
[33] W.S. McCulloch, W. Pitts, A logical calculus of the ideas immanent in nervous activity, The Bulletin of Mathematical Biophysics 5 (4) (1943) 115–133.
[34] S. Qian, H. Liu, C. Liu, S. Wu, H. San Wong, Adaptive activation functions in convolutional neural networks, Neurocomputing 272 (2018) 204–212.
[35] X. Jiang, Y. Pang, X. Li, J. Pan, Y. Xie, Deep neural networks with elastic rectified linear units for object recognition, Neurocomputing 275 (2018) 1132–1139.
[36] F. Fan, J. Xiong, G. Wang, Universal approximation with quadratic deep networks, Neural Networks 124 (2020) 383–392.
[37] D.T. Tran, S. Kiranyaz, M. Gabbouj, A. Iosifidis, Knowledge transfer for face verification using heterogeneous generalized operational perceptrons, in: 2019 IEEE International Conference on Image Processing (ICIP), IEEE, 2019, pp. 1168–1172.
[38] D.T. Tran, A. Iosifidis, Learning to rank: a progressive neural network learning approach, in: ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), IEEE, 2019, pp. 8355–8359.
[39] D. Thanh Tran, J. Kanniainen, M. Gabbouj, A. Iosifidis, Data-driven neural architecture learning for financial time-series forecasting, arXiv preprint, arXiv:1903.06751, 2019.
[40] D.T. Tran, S. Kiranyaz, M. Gabbouj, A. Iosifidis, Pygop: a Python library for generalized operational perceptron algorithms, Knowledge-Based Systems 182 (2019) 104801.
[41] D.T. Tran, M. Gabbouj, A. Iosifidis, Subset sampling for progressive neural network learning, in: Proceedings of the IEEE International Conference on Image Processing, 2020.
[42] B. Settles, Active learning literature survey, Tech. Rep., University of Wisconsin– Madison Department of Computer Sciences, 2009.
[43] V. Birodkar, H. Mobahi, S. Bengio, Semantic redundancies in image-classification datasets: the 10% you don’t need, arXiv preprint, arXiv:1901.11409, 2019.
[44] H. Shokri-Ghadikolaei, H. Ghauch, C. Fischione, M. Skoglund, Learning and data selection in big datasets, in: 36th International Conference on Machine Learning, Long Beach, California, PMLR 97, 2019, 2019.
[45] E.J. Candes, J.K. Romberg, T. Tao, Stable signal recovery from incomplete and inaccurate measurements, Communications on Pure and Applied Mathematics: A Journal Issued by the Courant Institute of Mathematical Sciences 59 (8) (2006) 1207–1223.
[46] D.L. Donoho, Compressed sensing, IEEE Transactions on Information Theory 52 (4) (2006) 1289–1306.
[47] E.J. Candès, M.B. Wakin, An introduction to compressive sampling, IEEE Signal Processing Magazine 25 (2) (2008) 21–30.
[48] M.A. Davenport, M.F. Duarte, M.B. Wakin, J.N. Laska, D. Takhar, K.F. Kelly, R.G. Baraniuk, The smashed filter for compressive classification and target recognition, in: Computational Imaging V, vol. 6498, International Society for Optics and Photonics, 2007, p. 64980H.
[49] K. Kulkarni, P. Turaga, Reconstruction-free action inference from compressive imagers, IEEE Transactions on Pattern Analysis and Machine Intelligence 38 (4) (2015) 772–784.
[50] S. Lohit, K. Kulkarni, P. Turaga, J. Wang, A.C. Sankaranarayanan, Reconstruction-free inference on compressive measurements, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, 2015, pp. 16–24.
[51] R.G. Baraniuk, M.B. Wakin, Random projections of smooth manifolds, Foundations of Computational Mathematics 9 (1) (2009) 51–77.
[52] R. Calderbank, S. Jafarpour, Finding needles in compressed haystacks, in: 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), IEEE, 2012, pp. 3441–3444.
[53] H. Reboredo, F. Renna, R. Calderbank, M.R. Rodrigues, Compressive classification, in: 2013 IEEE International Symposium on Information Theory, IEEE, 2013, pp. 674–678.
[54] S. Lohit, K. Kulkarni, P. Turaga, Direct inference on compressive measurements using convolutional neural networks, in: 2016 IEEE International Conference on Image Processing (ICIP), IEEE, 2016, pp. 1913–1917.
[55] A. Adler, M. Elad, M. Zibulevsky, Compressed learning: a deep neural network approach, arXiv preprint, arXiv:1610.09615, 2016.
[56] E. Zisselman, A. Adler, M. Elad, Compressed learning for image classification: a deep neural network approach, in: Handbook of Numerical Analysis, vol. 19, Elsevier, 2018, pp. 3–17.
[57] B. Hollis, S. Patterson, J. Trinkle, Compressed learning for tactile object recognition, IEEE Robotics and Automation Letters 3 (3) (2018) 1616–1623.
[58] A. De ̆gerli, S. Aslan, M. Yamac, B. Sankur, M. Gabbouj, Compressively sensed image recognition, in: 2018 7th European Workshop on Visual Information Processing (EUVIP), IEEE, 2018, pp. 1–6.
[59] Y. Xu, K.F. Kelly, Compressed domain image classification using a multi-rate neural network, arXiv preprint, arXiv:1901.09983, 2019.
[60] D.T. Tran, M. Yamaç, A. Degerli, M. Gabbouj, A. Iosifidis, Multilinear compressive learning, IEEE Transactions on Neural Networks and Learning Systems (2020).
[61] L. De Lathauwer, B. De Moor, J. Vandewalle, A multilinear singular value decomposition, SIAM Journal on Matrix Analysis and Applications 21 (4) (2000) 1253–1278.
[62] D.T. Tran, M. Gabbouj, A. Iosifidis, Multilinear compressive learning with prior knowledge, arXiv preprint, arXiv:2002.07203, 2020.
[63] G. Hinton, O. Vinyals, J. Dean, Distilling the knowledge in a neural network, arXiv preprint, arXiv:1503.02531, 2015.
[64] D.T. Tran, M. Gabbouj, A. Iosifidis, Performance indicator in multilinear compressive learning, in: Proceedings of the IEEE Symposium Series on Computational Intelligence, 2020.